Câu hỏi:

25/04/2023 2,244

Cho tam giác ABC bất kì, gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. H, H' lần lượt là trực tâm của tam giá ABC, MNP. Điểm K đối xứng H qua H'. Khẳng định nào sau đây đúng?

A. \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HH'} \)

B. \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HK} \)

C. \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow 0 \)

D. \(\overrightarrow {HM} + \overrightarrow {HN} + \overrightarrow {HP} = \overrightarrow {H'K} \)

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là B

Cho tam giác ABC bất kì, gọi M, N, P lần lượt là trung điểm của các cạnh (ảnh 1)

Xét tam giác ABC có M là trung điểm AB, N là trung điểm BC

Suy ra MN là đường trung bình

Do đó MN // AC, MN = \(\frac{1}{2}\)AC

Xét tam giác ABC có P là trung điểm AC, N là trung điểm BC

Suy ra PN là đường trung bình

Do đó PN // AB, PN = \(\frac{1}{2}\)AB

Xét tứ giác APNM có

AP // MN, AM // PN

Suy ra APNM là hình bình hành

Do đó \(\widehat {BAC} = \widehat {MNP}\)

Xét tam giác ABC và tam giác NPM có

\(\frac{{AB}}{{NP}} = \frac{{AC}}{{MN}} = 2\)

\(\widehat {BAC} = \widehat {MNP}\)

Suy ra (c.g.c) theo tỉ lệ là 2

Mà H, H’ là trực tâm tam giác ABC và tam giác NPM

Suy ra \(\frac{{CH}}{{MH'}} = 2\)

Hay CH = 2MH’ (1)

Mặt khác CH ⊥ AB, MH’⊥ PN, AB // PN

Suy ra MH’ // CH (2)

Từ (1) và (2) suy ra \(\overrightarrow {CH} = 2\overrightarrow {H'M} \)

Ta có \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HH'} + \overrightarrow {H'A} + \overrightarrow {HH'} + \overrightarrow {H'B} + \overrightarrow {HC} \)

\( = 2\overrightarrow {HH'} + (\overrightarrow {H'A} + \overrightarrow {H'B} ) + \overrightarrow {HC} = 2\overrightarrow {HH'} + (\overrightarrow {H'A} + \overrightarrow {AM} + \overrightarrow {H'B} + \overrightarrow {BM} ) + \overrightarrow {HC} \)

\( = 2\overrightarrow {HH'} + (\overrightarrow {H'M} + \overrightarrow {H'M} ) + \overrightarrow {HC} = 2\overrightarrow {HH'} + 2\overrightarrow {H'M} + \overrightarrow {HC} \)

\( = 2\overrightarrow {HH'} + \overrightarrow {CH} + \overrightarrow {HC} = 2\overrightarrow {HH'} = \overrightarrow {HK} \)

Vậy ta chọn đáp án B.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R):

a) y = f(x) = \(\frac{{3x + 1}}{{{x^2} + 2(m - 1)x + {m^2} + 3m + 5}}\)

b) y = f(x) = \(\sqrt {{x^2} + 2\left( {m - 1} \right)x + {m^2} + m - 6} \)

c) y = f(x) = \(\frac{{3x + 5}}{{{x^2} - 2(m + 3)x + m + 9}}\)

Xem đáp án

Lời giải

a) Hàm số f(x) luôn xác định trên R

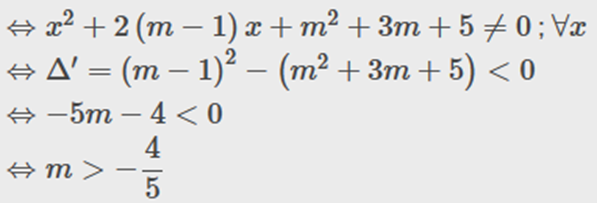
Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R) (ảnh 1)

Vậy m > \(\frac{{ - 4}}{5}\).

b) Hàm số f(x) luôn xác định trên R

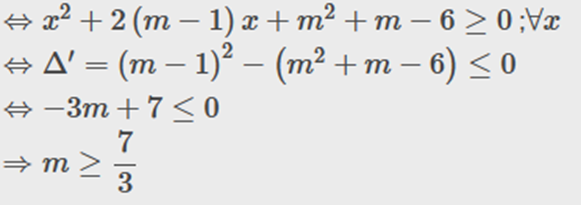
Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R) (ảnh 2)

Vậy m ≥ \(\frac{7}{3}\).

c) ) Hàm số f(x) luôn xác định trên R

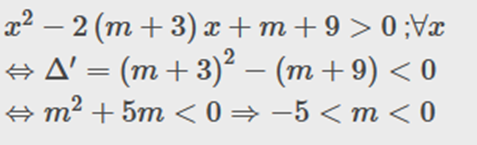
Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R) (ảnh 3)

Vậy – 5 < m < 0.

Câu 2

Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:

\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \)

Xem đáp án

Lời giải

Ta có :

\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CF} + \overrightarrow {FD} + \overrightarrow {EB} + \overrightarrow {BF} \)

\( = (\overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} ) + (\overrightarrow {FD} + \overrightarrow {DB} + \overrightarrow {BF} ) = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} + \overrightarrow {FF} \)

\( = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} + \overrightarrow 0 = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \)

Vậy \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \).

Câu 3

Cho tam giác ABC có AB = 2, BC = 4, CA = 3.

a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \), rồi suy ra cosA

b) Gọi G là trọng tâm của △ABC. Tính \(\overrightarrow {AG} .\overrightarrow {BC} \)

c) Tính giá trị biểu thức S = \(\overrightarrow {GA} .\overrightarrow {GB} + \overrightarrow {GB} .\overrightarrow {GC} + \overrightarrow {GC} .\overrightarrow {GA} \)

d) Gọi AD là phân giác trong của góc BAC (D ∈ BC). Tính \(\overrightarrow {A{\rm{D}}} \) theo \(\overrightarrow {AB} ;\overrightarrow {AC} \)suy ra AD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tỉ lệ phế phẩm của một nhà máy là 5%. Tìm xác xuất để trong 12 sản phẩm do nhà máy đó sản xuất ra có

a) 2 phế phẩm

b) không quá 2 phế phẩm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một thiết bị gồm có 3 bộ phận. Trong khoảng thời gian T, việc các bộ phận đó bị hỏng là độc lập với nhau và với các xác suất tương ứng là: 0,1; 0,2; 0,3. Cả thiết bị sẽ bị hỏng nếu có ít nhất một bộ phận hư hỏng. Tìm xác suất thiết bị hoạt động tốt trong thời gian T đó.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Tìm tập xác định của hàm số sau:

a) y = 3x² – 2x + 1

b) y = \(\frac{{3\left| x \right| + 2}}{{x - 2}}\)

c) y = \(\sqrt {x - 2} + \sqrt {3 - x} \)

d) y = \(\frac{{\frac{{2{\rm{x}} - 1}}{{\sqrt {4 - 3{\rm{x}}} }}}}{x}\)

e) y = \(\frac{{\sqrt {x + 3} }}{{2 - x}}\)

f) y = \(\frac{{2{\rm{x}} + 1}}{{{x^2} - 3{\rm{x}} + 2}}\)

g) y = \(\frac{{x - 1}}{{{x^2} - 1}} - 3x\)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một chiếc cổng hình parabol dạng y = \( - \frac{1}{2}{x^2}\) có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (Xem hình minh họa bên cạnh)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho tam giác ABC bất kì, gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. H, H' lần lượt là trực tâm của tam giá ABC, MNP. Điểm K đối xứng H qua H'. Khẳng định nào sau đây đúng?

Bình luận

Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \)

Tỉ lệ phế phẩm của một nhà máy là 5%. Tìm xác xuất để trong 12 sản phẩm do nhà máy đó sản xuất ra có a) 2 phế phẩm b) không quá 2 phế phẩm.

Một chiếc cổng hình parabol dạng y = \( - \frac{1}{2}{x^2}\) có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (Xem hình minh họa bên cạnh)

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:

\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \)

Tỉ lệ phế phẩm của một nhà máy là 5%. Tìm xác xuất để trong 12 sản phẩm do nhà máy đó sản xuất ra có

a) 2 phế phẩm

b) không quá 2 phế phẩm.