Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chứng minh rằng với điểm O bất kì, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).
Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chứng minh rằng với điểm O bất kì, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
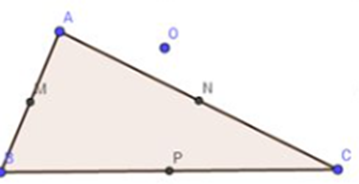
Vì M là trung điểm của AB nên \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \)
Vì N là trung điểm của AC nên \(\overrightarrow {OA} + \overrightarrow {OC} = 2\overrightarrow {ON} \)
Vì P là trung điểm của BC nên \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OP} \)
Suy ra \(2\overrightarrow {OA} + 2\overrightarrow {OB} + 2\overrightarrow {OC} = 2\overrightarrow {OM} + 2\overrightarrow {ON} + 2\overrightarrow {OP} \)
Hay \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \)
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Hàm số f(x) luôn xác định trên R
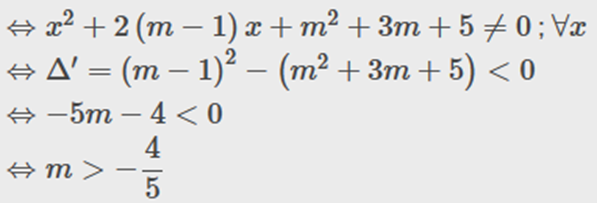
Vậy m > \(\frac{{ - 4}}{5}\).
b) Hàm số f(x) luôn xác định trên R
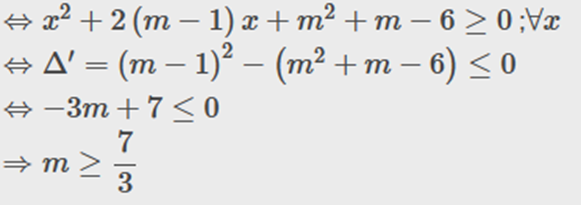
Vậy m ≥ \(\frac{7}{3}\).
c) ) Hàm số f(x) luôn xác định trên R
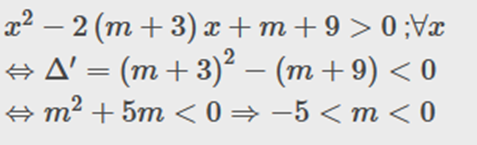
Vậy – 5 < m < 0.
Lời giải
Ta có :
\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CF} + \overrightarrow {FD} + \overrightarrow {EB} + \overrightarrow {BF} \)
\( = (\overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} ) + (\overrightarrow {FD} + \overrightarrow {DB} + \overrightarrow {BF} ) = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} + \overrightarrow {FF} \)
\( = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} + \overrightarrow 0 = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \)
Vậy \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.