5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 14)

🔥 Đề thi HOT:

2533 người thi tuần này

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

63.8 K lượt thi 126 câu hỏi

1756 người thi tuần này

135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

15.1 K lượt thi 35 câu hỏi

1164 người thi tuần này

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

13.2 K lượt thi 20 câu hỏi

1037 người thi tuần này

56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án

9.2 K lượt thi 56 câu hỏi

999 người thi tuần này

79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án

10.9 K lượt thi 40 câu hỏi

926 người thi tuần này

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

9.9 K lượt thi 15 câu hỏi

918 người thi tuần này

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)

63.9 K lượt thi 304 câu hỏi

905 người thi tuần này

87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án

10.1 K lượt thi 40 câu hỏi

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

19702 lượt thi

8 đề

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

15546 lượt thi

8 đề

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

16792 lượt thi

7 đề

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

15144 lượt thi

7 đề

225 Bài tập Số phức ôn thi Đại học có lời giải

11279 lượt thi

8 đề

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

23749 lượt thi

10 đề

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

21189 lượt thi

9 đề

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

13143 lượt thi

8 đề

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

7593 lượt thi

7 đề

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

6264 lượt thi

3 đề

Danh sách câu hỏi:

Câu 1

Cho tam giác ABC vuông tại A có . Gọi M và N lần lượt là trung điểm của BC và AC.

a) Tính góc .NMC.

b) Gọi E là điểm đối xứng với M qua N. Chứng minh tứ giác AECM là hình thoi.

c) Lấy D là điểm đối xứng với E qua BC. Tứ giác ACDB là hình gì? Tại sao?

d) Tam giác ABC có điều kiện gì thì tứ giác AECM là hình vuông?

Xem đáp án

Lời giải

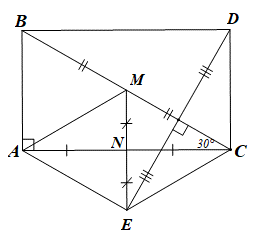
Media VietJack

a) Xét DABC vuông tại A có: \(\widehat B + \widehat C = 90^\circ \)

Suy ra \(\widehat B = 90^\circ - \widehat C = 90^\circ - 30^\circ = 60^\circ \).

Vì M, N lần lượt là trung điểm của BC, AC nên MN là đường trung bình của DABC.

Suy ra MN // AB nên \(\widehat {NMC} = \widehat B = 60^\circ \).

b) Ta có: E là điểm đối xứng với M qua N nên N là trung điểm của ME.

Lại có N là trung điểm của AC

Do đó tứ giác AECM có hai đường chéo AC, ME cắt nhau tại trung điểm N của mỗi đường nên là hình bình hành.

Mặt khác MN // AB và AB ⊥ AC nên MN ⊥ AC tại N.

Khi đó hình bình hành AECM có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường

Suy ra hình bình hành AECM là hình thoi.

c) • Ta có E, D đối xứng qua BC

Suy ra CE = CD nên DECD cân tại C

Khi đó đường cao CM đồng thời là đường phân giác của DECD

Suy ra \[\widehat {BCD} = \widehat {BCE}\]

Vì AECM là hình thoi nên CA là tia phân giác của góc ECM

Do đó \[\widehat {BCE} = 2.\widehat {ACB} = 60^\circ \].

Khi đó \[\widehat {BCD} = 60^\circ \].

Ta có \[\widehat {ACD} = \widehat {ACB} + \widehat {BCD} = 30^\circ + 60^\circ = 90^\circ \].

Hay CD ⊥ AC.

Mà AB ⊥ AC nên AB // DC.

• Mặt khác, DABC vuông tại A, có đường trung tuyến AM nên \(AM = \frac{1}{2}BC\).

DABC vuông tại A, có \(\widehat B = 60^\circ \) nên \(AB = \frac{1}{2}BC\).

Do đó AM = AB.

Lại có AECM là hình thoi nên AM = CE.

Khi đó: AB = AM = CE = CD.

• Xét tứ giác ABDC có AB // CD và AB = CD nên là hình bình hành.

Lại có \(\widehat {BAC} = 90^\circ \) nên ABDC là hình chữ nhật.

d) Do ABDC là hình chữ nhật nên hai đường chéo AD và BC cắt nhau tại trung điểm của mỗi đường.

Mà M là trung điểm của BC

Do đó M là trung điểm của AD hay A, M, D thẳng hàng.

Để tứ giác AECM là hình vuông thì AD ⊥ BC tại M

Điều này xảy ra khi và chỉ khi DABC có đường trung tuyến AM đồng thời là đường cao, tức là ΔABC vuông cân tại A.

Câu 2

Tìm a để hai đường thẳng (d₁): y = (a – 1)x + 1 và (d₂): y = (3 – a)x + 2 cắt nhau tại 1 điểm trên trục hoành.

Xem đáp án

Lời giải

• Để (d₁): y = (a – 1)x + 1 và (d₂): y = (3 – a)x + 2 cắt nhau thì a – 1 ≠ 3 – a

Û 2a ≠ 4 Û a ≠ 2.

• Để (d₁) cắt trục hoành thì a – 1 ≠ 0 Û a ≠ 1.

Gọi A(x_A; 0) là giao điểm của (d₁) với trục hoành.

Khi đó 0 = (a – 1)x_A + 1

Þ \({x_A} = \frac{{ - 1}}{{a - 1}}\). Suy ra \(A\left( {\frac{{ - 1}}{{a - 1}};0} \right)\).

• Để (d₂) cắt trục hoành thì 3 – a ≠ 0 Û a ≠ 3.

Gọi B(x_B; 0) là giao điểm của (d₂) với trục hoành.

Khi đó 0 = (3 – a)x_B + 2

Þ \({x_B} = \frac{{ - 2}}{{3 - a}} = \frac{2}{{a - 3}}\). Suy ra \(B\left( {\frac{2}{{a - 3}};0} \right)\).

Để (d₁) và (d₂) cắt nhau tại 1 điểm trên trục hoành thì A trùng B.

\( \Leftrightarrow \frac{{ - 1}}{{a - 1}} = \frac{2}{{a - 3}}\)

Þ ‒1.(a – 3) = 2.(a – 1)

Û ‒a + 3 = 2a – 2

Û ‒3a = ‒5

Û \(a = \frac{5}{3}\) (thỏa mãn).

Vậy \(a = \frac{5}{3}\) thỏa mãn yêu cầu đề bài.

Câu 3

Cho (d₁): y = (2m + 1)x – 2m – 3 và (d₂): y = (m – 1)x + m. Tìm m để (d₁) và (d₂) cắt nhau tại 1 điểm nằm trên trục hoành.

Xem đáp án

Lời giải

• Để (d₁): y = (2m + 1)x – 2m – 3 và (d₂): y = (m – 1)x + m cắt nhau thì 2m + 1 ≠ m – 1

Û m ≠ ‒2.

• Để (d₁) cắt trục hoành thì 2m + 1 ≠ 0 Û \(m \ne - \frac{1}{2}\).

Gọi A(x_A; 0) là giao điểm của (d₁) với trục hoành.

Khi đó 0 = (2m + 1)x_A – 2m – 3

Þ \({x_A} = \frac{{2m + 3}}{{2m + 1}}\). Suy ra \(A\left( {\frac{{2m + 3}}{{2m + 1}};0} \right)\).

• Để (d₂) cắt trục hoành thì m – 1 ≠ 0 Û m ≠ 1.

Gọi B(x_B; 0) là giao điểm của (d₂) với trục hoành.

Khi đó 0 = (m – 1)x_B + m

Þ \({x_B} = \frac{{ - m}}{{m - 1}}\). Suy ra \(B\left( {\frac{{ - m}}{{m - 1}};0} \right)\).

Để (d₁) và (d₂) cắt nhau tại 1 điểm trên trục hoành thì A trùng B.

\( \Leftrightarrow \frac{{2m + 3}}{{2m + 1}} = \frac{{ - m}}{{m - 1}}\)

Þ (2m + 3).(m – 1) = (2m + 1).(‒m)

Û 2m² + m – 3 = –2m² – m

Û 4m² + 2m – 3 = 0

Û \(m = \frac{{ - 1 \pm \sqrt {13} }}{4}\) (thỏa mãn).

Vậy \(m = \frac{{ - 1 \pm \sqrt {13} }}{4}\) thỏa mãn yêu cầu đề bài.

Câu 4

Trong phép tính 121,23 : 14 và có thương là 8,65 vậy số dư là bao nhiêu?

A. 13;

B. 1,3;

C. 0,13;

D. 0,013.

Lời giải

Đáp án đúng là: C

Ta có: Số bị chia = Số chia × Thương + Số dư

Số dư = Số bị chia – Số chia × Thương

= 121,23 – 14 × 8,65

= 121,23 – 121,1

= 0,13.

Câu 5

Tìm số dư của phép chia 121,23 : 14 biết thương lấy đến hai chữ số ở phần thập phân.

Xem đáp án

Lời giải

Đặt tính chia: 121,23 : 14 như sau:

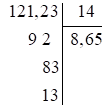
Media VietJack

Vậy số dư cần tìm là: 0,13.

Câu 6

Cho a + b = 1 và ab ≠ 0. Chứng minh \(\frac{a}{{{b^3} - 1}} + \frac{b}{{{a^3} - 1}} = \frac{{2.\left( {ab - 2} \right)}}{{{a^2}{b^2} + 3}}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho tam giác ABC vuông tại A (AB < AC) có D và E lần lượt là trung điểm của các cạnh AC và BC. Vẽ EF vuông góc với AB tại F.

a) Chứng minh rằng DE //AB và tứ giác ADEF là hình chữ nhật.

b) Trên tia đối của tia DE lấy điểm G sao cho DG = DE. Chứng minh tứ giác AECG là hình thoi.

c) Gọi O là giao điểm của AE và DF. Chứng minh rằng ba điểm B, O, G thẳng hàng.

d) Vẽ EH vuông góc với AG tại H. Chứng minh rằng tam giác DHF vuông.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Tính m để 3 điểm thẳng hàng:

a) A(2; 5), B(3; 7), C(2m + 1; m);

b) A(2m; ‒5), B(0; m), C(2; 3);

c) A(3; 7), B(m²; m), C(‒1; ‒1).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Tìm m để ba điểm A(2; ‒1), B(1; 1), C(3; m +1) thẳng hàng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Cho phương trình x² – 2x – 2m² = 0 (m là tham số).

a) Giải phương trình khi m = 0.

b) Tìm m để phương trình có hai nghiệm x₁, x₂ khác 0 và thỏa mãn điều kiện \(x_1^2 = 4x_2^2\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt x₁, x₂ khác 0 khi nào?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Một can nước (tính cả vỏ can) nặng 12 kg. Sau đó người ta đổ bớt \(\frac{1}{3}\) số nước ra ngoài. Biết rằng can rỗng nặng 600 g. Hỏi sau khi đổ bớt nước ra ngoài, can nước cân nặng bao nhiêu?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Một can nước (tính cả vỏ can) nặng 12 kg. Sau đó người ta đổ bớt \(\frac{1}{3}\) số nước ra ngoài. Biết rằng can rỗng nặng 600 g. Cân nặng của can nước còn lại là bao nhiêu?

A.8 kg;

B. 8,2 kg;

C. 820 dag;

D.800 dag.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Trong mặt phẳng tọa độ Oxy, cho vectơ \(\overrightarrow a = \left( {9;3} \right)\). Vectơ nào sau đây không vuông góc với vectơ \(\overrightarrow a \)?

A. \({\overrightarrow v _1} = \left( {1; - 3} \right)\);

B. \({\overrightarrow v _2} = \left( {2; - 6} \right)\);

C. \({\overrightarrow v _3} = \left( {1;3} \right)\);

D. \({\overrightarrow v _4} = \left( { - 1;3} \right)\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Trong mặt phẳng Oxy, với giá trị nào của m thì đường thẳng D₁: (2m – 1)x + my – 10 = 0 vuông góc với đường thẳng D₂: 3x + 2y + 6 = 0?

A. m = 0;

B. m ∈ ∅;

C. m = 2;

D. \(m = \frac{3}{8}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Viết các ước của 58.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Tìm x biết \(\left| {x + \frac{1}{3}} \right| - 4 = - 1\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Tìm số hữu tỉ x, biết:

a) \(\left| {x + \frac{1}{3}} \right| - 4 = - 1\).

b) \(1\frac{3}{4}x + 1\frac{1}{2} = - \frac{4}{5}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Cho tam giác ABC có G là trọng tâm, I là trung điểm của đoạn thẳng BC. Đẳng thức nào sau đây là đúng?

A. \[\overrightarrow {GA} = 2\overrightarrow {GI} \];

B. \(\overrightarrow {IG} = \frac{{ - 1}}{3}\overrightarrow {IA} \);

C. \[\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GI} \];

D. \[\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} \].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Cho nửa đường tròn tâm O có đường kính AB, Ax là tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn nằm cùng phía đối với AB), C là một điểm thuộc nửa đường tròn, H là hình chiếu của C trên AB. Đường thẳng qua O và vuông góc với AC cắt Ax tại M. Gọi I là giao điểm của MB và CH. Chứng minh rằng CI = IH.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C khác A, B) vẽ tiếp tuyến CM cắt Ax tại M, hạ CH vuông góc với AB, MB cắt (O) tại Q và cắt CH tại N.

a) Chứng minh MA² = MQ.MB.

b) MO cắt AC tại I. Chứng minh tứ giác AIQM nội tiếp.

c) Chứng minh: IN vuông góc CH.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Cho tam giác ABC có AB = a, AC = 2a. Gọi D là trung điểm AC, M là điểm thỏa mãn \(\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} \). Chứng minh: BD vuông góc AM.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Cho 3 số dương x, y, x thỏa mãn x + y + z = 3.

Tìm giá trị nhỏ nhất của \(P = \frac{1}{{yz}} + \frac{1}{{xz}}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Cho nửa đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường tròn (O) lấy một điểm E bất kì (E khác A, B). Tiếp tuyến tại E của đường tròn (O) cắt Ax, By lần lượt tại C, D.

a) Chứng minh: CD = AC + BD.

b) Vẽ EF vuông góc AB tại F, BE cắt AC tại K. Chứng minh: AF.AB = KE.EB.

c) EF cắt CB tại I. Chứng minh , suy ra FE là tia phân giác của góc CFD.

d) EA cắt CF tại M, EB cắt DF tại N. Chứng minh: M, I, N thẳng hàng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Cho nửa đường tròn (O), đường kính AB, vẽ các tiếp tuyến Ax, By của nửa đường tròn (O). Từ điểm M trên nửa đường tròn (M khác A, B) vẽ tiếp tuyến thứ ba của nửa đường tròn (O), cắt Ax ở C và cắt By ở D. Gọi N là giao điểm của BC và AD. Chứng minh rằng:

a) \(\frac{{CN}}{{AC}} = \frac{{NB}}{{BD}}\).

b) MN ⊥ AB.

c) \[\widehat {COD} = 90^\circ \].

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Cho nửa đường tròn (O; R) đường kính AB. Điểm C thuộc nửa đường tròn sao cho AC > CB, C khác A và B. Kẻ CH vuông góc với AB tại H. Kẻ OI vuông góc với AC tại I.

a) Chứng minh bốn điểm C, H, O, I cùng thuộc một đường tròn.

b) Kẻ tiếp tuyến Ax của đường tròn (O; R), tia OI cắt Ax tại M, chứng minh OI.OM = R². Tính độ dài đoạn thẳng OI biết OM = 2R và R = 6 cm.

c) Gọi giao điểm của BM với CH là K. Chứng minh tam giác AMO đồng dạng với tam giác HCB và KC = KH.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Cho 6 điểm A, B, C, D, E, F. Hãy chứng minh các đẳng thức sau bằng nhiều cách khác nhau:

a) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DE} = \overrightarrow {AE} \);

b) \(\overrightarrow {AB} - \overrightarrow {AC} + \overrightarrow {DE} - \overrightarrow {DF} = \overrightarrow {FB} + \overrightarrow {CE} \).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Hình thoi ABCD có diện tích 20 cm² và đường chéo AC bằng 10 cm. Tính độ dài đường chéo BD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Tìm tập xác định của hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\sqrt { - 3x + 8} + x\,\,\,khi\,\,x < 2\\\sqrt {x + 7} + 1\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 2\end{array} \right.\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Giải phương trình \({x^2} - 1 = 2\sqrt {2x + 1} \).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Cho tam giác ABC cân tại đỉnh A. Gọi H là trung điểm của BC, D là hình chiếu của H lên AC, M là trung điểm của HD. Chứng minh rằng: AM ⊥ DB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Cho tam giác ABC nhọn, vẽ đường tròn \(\left( {O;\frac{1}{2}BC} \right)\) cắt các cạnh AB, AC theo thứ tự tại D và E.

a) Chứng minh rằng: CD vuông góc với AB, BE vuông góc với AC.

b) Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc với BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

Cho hai hàm số bậc nhất có đồ thị là (D): y = (5m – 2)x – 3 và (D'): y = –x + 3 – 2m. Tìm m để (D) và (D') cắt nhau tại 1 điểm trên trục hoành.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

Tìm giá trị của m để hai đồ thị hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại 1 điểm trên trục hoành.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

Cho tam giác ABC vuông tại A, đường cao AH.

a) Chứng minh: AH.BC = AB.AC.

b) Gọi M là điểm nằm ở giữa B và C. Kẻ MN vuông với AB, MP vuông góc với AC (N thuộc AB, P thuộc AC ) tứ giác ANMP là hình gì? Vì sao?

c) Tính số đo góc NHP?

d) Tìm vị trí M trên BC để NP có độ dài ngắn nhất?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Từ M hạ MP vuông góc với AB (P ∈ AB), MQ vuông góc với AC (Q ∈ AC). Gọi R là điểm đối xứng M qua P.

a) Tứ giác AQMP là hình gì? Vì sao?

b) Tứ giác AMBR là hình gì? Vì sao?

c) Để tứ giác AQMP là hình vuông thì tam giác ABC cần thêm điều kiện gì?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Tích của hai số là 625. Nếu gấp thừa số thứ nhất lên 2 lần và gấp thừa số thứ hai lên 3 lần thì tích mới là bao nhiêu?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

Cho hàm số bậc nhất \(y = \frac{3}{4}x + 3\) có đồ thị là đường thẳng (d).

a) Vẽ (d) trên mặt phẳng toạ độ Oxy.

b) Tính khoảng cách từ gốc toạ độ O đến đường thẳng (d).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

Tìm tập xác định của hàm số \(y = \frac{{2x - 1}}{{\sqrt x - 2}}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

Tìm tập xác định của hàm số \(y = \frac{{2x - 1}}{{\sqrt {x - 2} }}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Không giải phương trình, tìm các nghiệm số của phương trình x³ – 15x² + 71x – 105 = 0, biết rằng các nghiệm số phân biệt và tạo thành một cấp số cộng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Cho hàm số y = 2x² – 3x – 5 (1). Tìm giá trị của tham số m để đồ thị hàm số (1) cắt đường thẳng y = 4x + m tại hai điểm phân biệt A(x₁; y₁), B(x₂; y₂) thỏa mãn \(2x_1^2 + 2x_2^2 = 3{x_1}{x_2} + 7\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

Cho tam giác ABC vuông tại A, đường cao AH. Biết diện tích các tam giác ABH và ACH lần lượt là 54 cm² và 96 cm². Độ dài BC là

A. 15 cm;

B. 25 cm;

C. 35 cm;

D. 45 cm.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

Cho tam giác ABC vuông tại A, đường cao AH. Biết diện tích các tam giác ABH và ACH lần lượt là 54 cm² và 96 cm². Tính AB, AC, BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

Cho tứ giác ABCD có AB = CD. Gọi E, F lần lượt là trung điểm của AC và BD. Đường thẳng EF lần lượt cắt AB, CD tại H, K. Chứng minh rằng \(\widehat {KHB} = \widehat {HKC}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Cho tứ giác ABCD có AB // CD và CD > AB. Gọi E, F lần lượt là trung điểm của AC và BD. Chứng minh rằng \(EF = \frac{{CD - AB}}{2}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

Trong một ngày trường A cần làm 120 cái lồng đèn ông trang trí trường nhân dịp Trung Thu. Biết rằng mỗi bạn nam làm được 2 cái và mỗi bạn nữ làm được 3 cái trong một ngày. Gọi x là số bạn nam, y là số bạn nữ được trường huy động làm.

a) Viết hàm số biểu diễn y theo x.

b) Nếu trường chỉ có thể huy động 15 bạn nam có khả năng làm thì cần huy động thêm bao nhiêu bạn nữ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

Cho phương trình x² – (m – 1)x – m = 0, trong đó m là tham số, x là ẩn số. Tìm m để phương trình có hai nghiệm phân biệt đều nhỏ hơn 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Tìm m để ba đường thẳng đồng quy.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

Cho ba đường thẳng y = 2x + 1 (d₁); y = x – 1 (d₂) và y = (m + 1)x – 2. Tìm điều kiện của tham số m để ba đường thẳng đồng quy.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 51

Cho ba đường thẳng y = x + 6 (d₁); y = 3x + 7 (d₂) và y = (2 – m)x + 1 (d₃). Tìm m để (d₁), (d₂) và (d₃) đồng quy.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 52

Nêu công thức tính số đo góc giữa hai vectơ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 53

Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) trong mỗi trường hợp sau:

a) \(\overrightarrow a = \left( { - 3;1} \right),\overrightarrow b = \left( {2;6} \right);\)

b) \(\overrightarrow a = \left( {3;1} \right),\overrightarrow b = \left( {2;4} \right);\)

c) \(\overrightarrow a = \left( { - \sqrt 2 ;1} \right),\overrightarrow b = \left( {2; - \sqrt 2 } \right).\)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 54

Cho tập X = {1; 2; 3; ....; 8}. Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để lập được số chia hết cho 1111 là

A. \(\frac{{C_8^2C_6^2C_4^2}}{{8!}}\);

B. \(\frac{{4!.4!}}{{8!}}\);

C. \(\frac{{384}}{{8!}}\);

D. \(\frac{{A_8^2A_6^2A_4^2}}{{8!}}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 55

Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 lập các số tự nhiên có tám chữ số đôi một khác nhau. Lấy ngẫu nhiên một số vừa lập. Xác suất để lấy được số chia hết cho 1111 là:

A. \(\frac{8}{{35}}\);

B. \(\frac{1}{{2520}}\);

C. \(\frac{1}{{630}}\);

D. \(\frac{1}{{105}}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 56

Chứng minh rằng a³b – ab³ chia hết cho 6 với mọi số nguyên a và b.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 57

Giải hệ phương trình \(\left\{ \begin{array}{l}{\left( {2xy - 1} \right)^2} + 4{x^2} = 5{y^2}\\2x\left( {x - {y^2}} \right) = {y^2} - y\end{array} \right.\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 58

Cho a, b > 0 thỏa mãn ab = 1. Chứng minh \(\frac{1}{a} + \frac{1}{b} + \frac{2}{{a + b}} \ge 3\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 59

Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM và CD = 2CN. Gọi G là trọng tâm của tam giác MNB. Phân tích các vectơ \(\overrightarrow {AN} ,\overrightarrow {MN} ,\overrightarrow {AG} \) qua các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 60

Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AB và CD sao cho AB = 3AM và CD = 2CN. Biểu diễn vectơ \(\overrightarrow {AN} \) qua các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

4.6

12356 Đánh giá

50%

40%

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 14)

🔥 Đề thi HOT: