Câu hỏi:
12/07/2024 1,205
Cho tứ giác ABCD có AB = CD. Gọi E, F lần lượt là trung điểm của AC và BD. Đường thẳng EF lần lượt cắt AB, CD tại H, K. Chứng minh rằng \(\widehat {KHB} = \widehat {HKC}\).
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
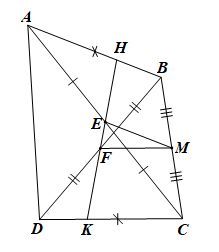
Gọi M là trung điểm của BC.
Xét DABC có E, M lần lượt là trung điểm của AC, BC nên EM là đường trung bình của tam giác
Suy ra EM // DC và \(EM = \frac{1}{2}AB\).
Chứng minh tương tự ta cũng có: FM là đường trung bình của tam giác BCD.
Suy ra FM // DC và \(FM = \frac{1}{2}DC\)
Mà theo bài, AB = CD nên EM = FM
Do đó tam giác EFM là tam giác cân tại M, suy ra \(\widehat {FEM} = \widehat {EFM}\).
Mặt khác, do EM // AB nên \(\widehat {FEM} = \widehat {KHB}\) (đồng vị);
FM // DC nên \(\widehat {EFM} = \widehat {HKC}\) (đồng vị).
Do đó \(\widehat {KHB} = \widehat {HKC}\) (điều phải chứng minh).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho (d1): y = (2m + 1)x – 2m – 3 và (d2): y = (m – 1)x + m. Tìm m để (d1) và (d2) cắt nhau tại 1 điểm nằm trên trục hoành.
Xem đáp án »
12/07/2024
17,655
Câu 3:
Cho phương trình x2 – 2x – 2m2 = 0 (m là tham số).
a) Giải phương trình khi m = 0.
b) Tìm m để phương trình có hai nghiệm x1, x2 khác 0 và thỏa mãn điều kiện \(x_1^2 = 4x_2^2\).
Cho phương trình x2 – 2x – 2m2 = 0 (m là tham số).
a) Giải phương trình khi m = 0.
b) Tìm m để phương trình có hai nghiệm x1, x2 khác 0 và thỏa mãn điều kiện \(x_1^2 = 4x_2^2\).
Xem đáp án »
12/07/2024
7,205
Câu 4:
Tìm tập xác định của hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\sqrt { - 3x + 8} + x\,\,\,khi\,\,x < 2\\\sqrt {x + 7} + 1\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 2\end{array} \right.\).
Xem đáp án »
11/07/2024
7,131
Câu 5:
Cho nửa đường tròn (O; R) đường kính AB. Điểm C thuộc nửa đường tròn sao cho AC > CB, C khác A và B. Kẻ CH vuông góc với AB tại H. Kẻ OI vuông góc với AC tại I.
a) Chứng minh bốn điểm C, H, O, I cùng thuộc một đường tròn.
b) Kẻ tiếp tuyến Ax của đường tròn (O; R), tia OI cắt Ax tại M, chứng minh OI.OM = R2. Tính độ dài đoạn thẳng OI biết OM = 2R và R = 6 cm.
c) Gọi giao điểm của BM với CH là K. Chứng minh tam giác AMO đồng dạng với tam giác HCB và KC = KH.
Cho nửa đường tròn (O; R) đường kính AB. Điểm C thuộc nửa đường tròn sao cho AC > CB, C khác A và B. Kẻ CH vuông góc với AB tại H. Kẻ OI vuông góc với AC tại I.
a) Chứng minh bốn điểm C, H, O, I cùng thuộc một đường tròn.
b) Kẻ tiếp tuyến Ax của đường tròn (O; R), tia OI cắt Ax tại M, chứng minh OI.OM = R2. Tính độ dài đoạn thẳng OI biết OM = 2R và R = 6 cm.
c) Gọi giao điểm của BM với CH là K. Chứng minh tam giác AMO đồng dạng với tam giác HCB và KC = KH.
Xem đáp án »
12/07/2024
4,821
Câu 6:
Cho a + b = 1 và ab ≠ 0. Chứng minh \(\frac{a}{{{b^3} - 1}} + \frac{b}{{{a^3} - 1}} = \frac{{2.\left( {ab - 2} \right)}}{{{a^2}{b^2} + 3}}\).
Xem đáp án »
12/07/2024
4,427
Câu 7:
Cho nửa đường tròn tâm O có đường kính AB, Ax là tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn nằm cùng phía đối với AB), C là một điểm thuộc nửa đường tròn, H là hình chiếu của C trên AB. Đường thẳng qua O và vuông góc với AC cắt Ax tại M. Gọi I là giao điểm của MB và CH. Chứng minh rằng CI = IH.
Xem đáp án »
12/07/2024
3,492
về câu hỏi!