Cho hình bình hành ABCD có tâm O. Tìm vecto từ 5 điểm A, B, C, D bằng \(\overrightarrow {AB} ;\,\,\overrightarrow {OB} \).
Cho hình bình hành ABCD có tâm O. Tìm vecto từ 5 điểm A, B, C, D bằng \(\overrightarrow {AB} ;\,\,\overrightarrow {OB} \).
A. \(\overrightarrow {AB} = \overrightarrow {AC} ,\overrightarrow {OB} = \overrightarrow {AO} \);
B. \(\overrightarrow {AB} = \overrightarrow {OC} ;\overrightarrow {OB} = \overrightarrow {DO} \);
C. \(\overrightarrow {AB} = \overrightarrow {DC} ;\overrightarrow {OB} = \overrightarrow {AO} \);
D. \(\overrightarrow {AB} = \overrightarrow {DC} ;\overrightarrow {OB} = \overrightarrow {DO} \).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D.
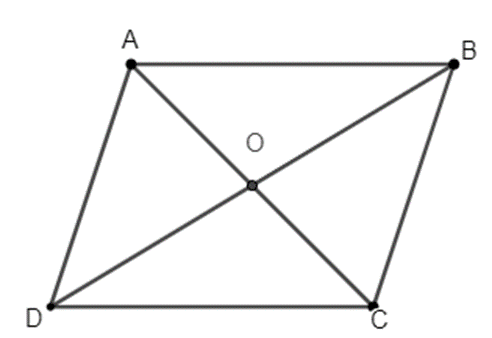
Vì ABCD là hình bình hành ta có: AB = DC; OB = OD.
Mà ta có hai vectơ bằng nhau nếu chúng cùng hướng và độ dài nên: \(\overrightarrow {AB} = \overrightarrow {DC} ;\,\,\overrightarrow {OB} = \overrightarrow {DO} \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
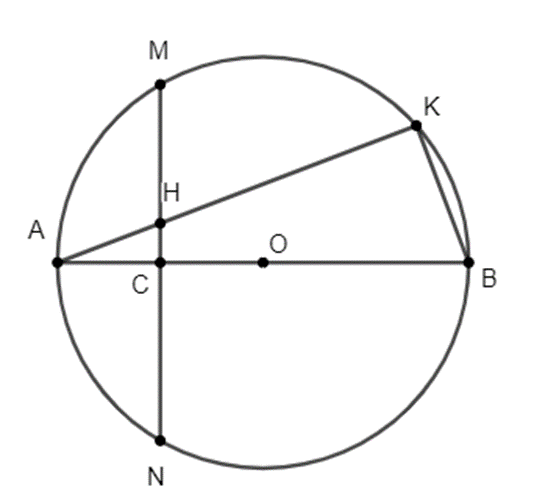
a) Ta có: \(\widehat {AKB} = 90^\circ \) (góc nội tiếp đường tròn (O)) \( \Rightarrow \widehat {HKB} = 90^\circ \).
Có: \(\widehat {ACH} = \widehat {HCB} = 90^\circ \) (MN\( \bot \)AB; H, C ∈ MN)
Xét tứ giác BCHK có \(\widehat {HCB} + \widehat {HKB} = 90^\circ + 90^\circ = 180^\circ \)
Suy ra tứ giác BCHK nội tiếp đường tròn.
b) Xét \(\Delta ACH\) và \(\Delta AKB\) có:
\(\widehat {BAK}\) chung
\(\widehat {ACH} = \widehat {AKB} = 90^\circ \) (cmt)
Suy ra \(\Delta AHC\) ᔕ \(\Delta AKB\)(g.g)
\( \Rightarrow \frac{{AH}}{{AB}} = \frac{{AC}}{{AK}}\)
\( \Leftrightarrow \)AH.AK = AC. AB \( = \frac{R}{2}.2R = {R^2}\) (đpcm)
Lời giải
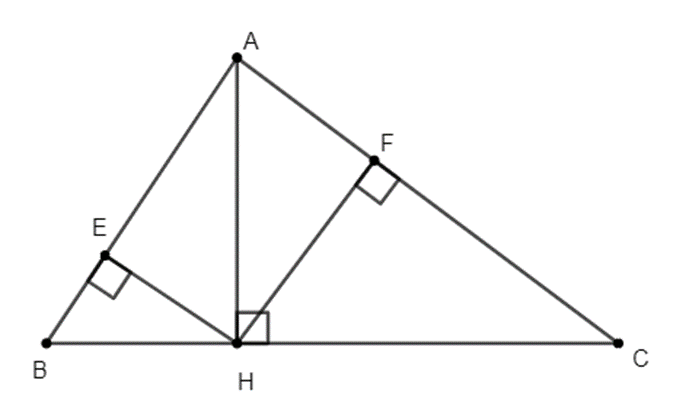
a) Áp dụng hệ thức lượng trong tam giác, ta có:
• Xét \(\Delta AHC\): AH2 = AF.AC
• Xét \(\Delta AHB\): AH2 = AE.AB
Do đó AE.AB = AF. AC
b) Ta có: AH2 = AE.AB
\( \Rightarrow AE = \frac{{A{H^2}}}{{AB}} = \frac{{{3^3}}}{4} = 2,25\) (cm)
Mà AE + BE = AB
\( \Rightarrow \)BE = AB – AE
= 4 – 2,24 = 1,75 (cm)
c) \(\Delta AHC\) vuông tại H
\( \Rightarrow \cos \widehat {HAC} = \frac{{AH}}{{AC}}\)
\(AC = \frac{6}{{\sqrt 3 }} = 2\sqrt 3 \) (cm)
Theo ý a) ta có: AE.AB = AF.AC
\( \Rightarrow AF = \frac{{AE.AB}}{{AC}} = \frac{{2,25.4}}{{2\sqrt 3 }} = \frac{{3\sqrt 3 }}{2}\)(cm)
FC = AC – AF
\( = 2\sqrt 3 - \frac{{3\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\)(cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.