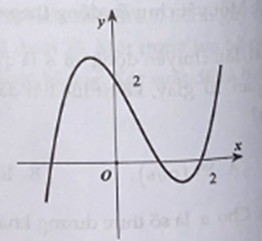
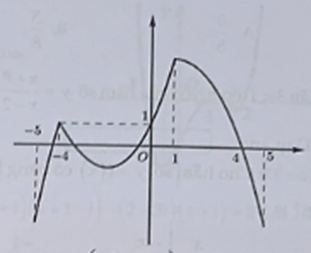
Cho hàm số y = f(x) có đồ thị như hình vẽ.
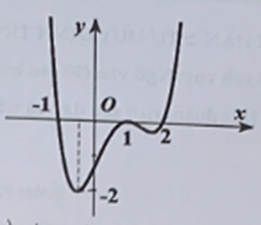
Đặt g(x) = f(f(x) - 1). Tìm số nghiệm của phương trình g'(x) = 0.
Cho hàm số y = f(x) có đồ thị như hình vẽ.

Đặt g(x) = f(f(x) - 1). Tìm số nghiệm của phương trình g'(x) = 0.
Câu hỏi trong đề: Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 2) !!
Quảng cáo
Trả lời:
Ta có
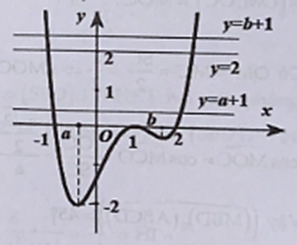
+) Với
+) Với
Từ đồ thị hàm số f(x) ta có:
- Phương trình (1) có 2 nghiệm.
- Phương trình (2) có 2 nghiệm không trùng với 2 nghiệm của phương trình (1).
- Phương trình (3) có 2 nghiệm không trùng với 2 nghiệm của phương trình (1) và 2 nghiệm của phương trình (2).
Vậy phương trình g'(x) = 0 có tất cả 9 nghiệm.Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
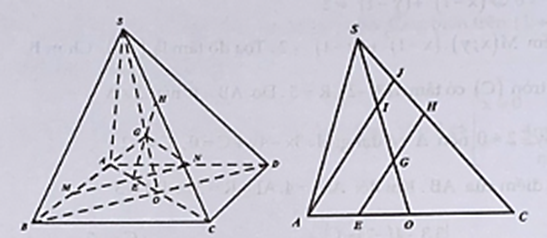
Trong mặt phẳng (ABCD), gọi . Trong mặt phẳng (SAC), gọi .
Ta có: .
Gọi I, J lần lượt là trung điểm của SG và SH .
Ta có A, I, J thẳng hàng. Xét có .
Lai có SH = 2HJ nên SC = 5HJ. VậyLời giải
Các phát biểu đúng là: (b), (c), (d), (e).
Phát biểu (a) không đúng vì chất rắn nổi lên là muối của natri với axit béo.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. m = -6
B. m = 0
C. m = -4
D. m = 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.