Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{1}{4}{x^4} - 14{x^2} + 48x + m - 30} \right|\) trên đoạn [0; 2] không vượt quá 30. Tính tổng các phần tử của S.
Quảng cáo
Trả lời:
Lời giải
Đặt \(f\left( x \right) = \frac{1}{4}{x^4} - 14{x^2} + 48x + m - 30\) là hàm số xác định và liên tục trên đoạn [0; 2]
Ta có: f ¢(x) = x3 − 28x + 48
Với mọi x Î [0; 2] ta có f ¢(x) = x3 − 28x + 48 = 0 Û x = 2
Mặt khác: f (0) = m − 30; f (x) = m + 14.
\(\mathop {\max }\limits_{\left[ {0;\;2} \right]} \left| {f\left( x \right)} \right| = \max \left\{ {\left| {f\left( 0 \right)} \right|;\;\left| {f\left( 2 \right)} \right|} \right\}\)
Theo bài ra ta có: \[\mathop {\max }\limits_{\left[ {0;\;2} \right]} \left| {f\left( x \right)} \right| \le 30 \Leftrightarrow \left\{ \begin{array}{l}\left| {f\left( 0 \right)} \right| \le 30\\\left| {f\left( 2 \right)} \right| \le 30\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}\left| {m - 30} \right| \le 30\\\left| {m + 14} \right| \le 30\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 30 \le m - 30 \le 30\\ - 30 \le m + 14 \le 30\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}0 \le m \le 60\\ - 44 \le m \le 16\end{array} \right. \Leftrightarrow 0 \le m \le 16\]
Do m Î ℤ Þ m Î S = {0; 1; 2; 3; 4; 5; …; 16}
Vậy tổng tất cả 17 giá trị trong tập S là \(\frac{{17\,.\,\left( {0 + 16} \right)}}{2} = 136\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Lời giải
Đáp án đúng là: B
Với góc a Î (90°; 180°) thì sin a > 0; cos a < 0; tan a < 0 và cot a < 0
Khi đó:
• sin a và cot a trái dấu
Vậy khẳng định A là sai
• Tích sin a.cot a mang dấu âm
Vậy khẳng định B là đúng
• Tích sin a.cos a mang dấu âm
Vậy khẳng định C là sai
• sin a và tan a trái dấu
Vậy khẳng định D là sai
Chọn đáp án B.
Lời giải
Lời giải
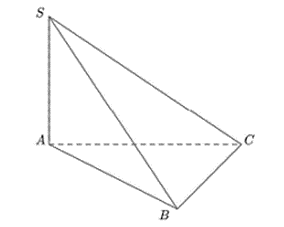
Ta có tam giác ABC vuông cân tại C nên BC ^ AC (1) và AC = BC = 3a
Mặt khác SA ^ (ABC) Þ SA ^ BC (2)
Từ (1) và (2) suy ra BC ^ (SAC) Þ d(B, (SAC)) = BC = 3a
Vậy khoảng cách từ B đến mặt phẳng (SAC) bằng 3a.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.