Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Kẻ 2 tiếp tuyến AM, AN và cát tuyến ABC với đường tròn (AB < AC). Qua O kẻ OK vuông góc với BC tại K, OK cắt MN tại S. Chứng minh SC là tiếp tuyến của đường tròn (O).
Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Kẻ 2 tiếp tuyến AM, AN và cát tuyến ABC với đường tròn (AB < AC). Qua O kẻ OK vuông góc với BC tại K, OK cắt MN tại S. Chứng minh SC là tiếp tuyến của đường tròn (O).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
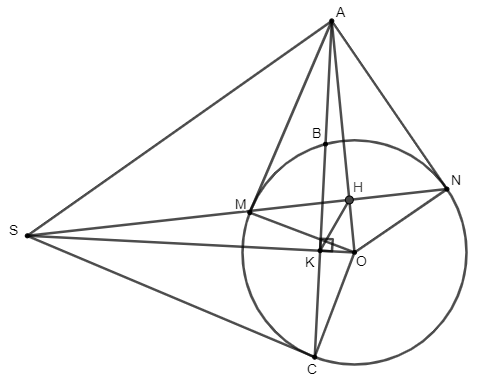
Gọi AO ∩ MN ≡ H
Theo tính chất hai tiếp tuyến cắt nhau: AM = AN
Mà OM = ON nên OA là trung trực của MN
Do đó OA ⊥ MN (1)
Mặt khác BC ⊥ OK ⟹ AC⊥ OS ⟹ (2)
Từ (1) và (2) suy ra tứ giác SKHA nội tiếp (hai góc cùng nhìn một cạnh bằng nhau)
Do đó theo tính chất tứ giác nội tiếp thì: OK.OS = OH.OA (*)
Vì AM là tiếp tuyến của đường tròn (O) nên AM ⊥ OM
Xét tam giác vuông AMO có đường cao MH, theo hệ thức lượng trong tam giác vuông thì: OC2 = R2 = OM2 = OH.OA (**)
Từ (*) và (**) ⟹ OC2 = OK.OS
Do đó tam giác OCK đồng dạng với tam giác OSC (cạnh – góc – cạnh)
⇒ SC ⊥ OC ⇒ SC là tiếp tuyến của đường tròn (O).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
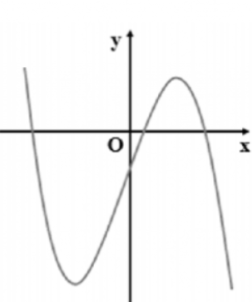
A. a > 0, d > 0;
B. a < 0, d > 0;
C. a > 0, d < 0;
D. a < 0, d < 0.
Lời giải
Đáp án đúng là: D
Ta có: đồ thị nhánh ngoài cùng của hàm số hướng đi xuống nên hệ số a < 0.
Giao điểm của đồ thị hàm số với trục tung Oy: x = 0 là điểm nằm bên dưới trục hoành nên khi x = 0 ⇒ y = d < 0
Vậy đáp án đúng là D.
Lời giải
Gọi Ω là không gian mẫu của phép thử: “Chọn ngẫu nhiên một số từ tập X”
Khi đó
Gọi A là biến cố: “Số được chọn chỉ chứa 3 chữ số lẻ”. Khi đó:
+ Chọn 3 chữ số lẻ đôi một khác nhau từ các chữ số 1; 3; 5; 7; 9 có cách
+ Chọn 3 chữ số chẵn đôi một khác nhau từ các chữ số 2; 4; 6; 8 có cách
+ Sắp xếp các chữ số trên để được số thỏa mãn biến cố A có 6! cách
Do đó
Vậy xác suất cần tìm là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.
B.
C. = a
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. C(5; -4);
B. C(5; 4);
C. C(-5; 4);
D. C(-5; -4).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập