Câu hỏi:

12/07/2024 3,765

Cho hình chóp S.ABC có SA vuông góc với đáy, SA = 2BC và góc $\hat{B A C} = 120^{°}$ . Hình chiếu vuông góc của A lên các đoạn SB và SC lần lượt là M và N. Tính góc giữa hai mặt phẳng (ABC) và (AMN).

Xem lời giải

Câu hỏi trong đề: Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 5) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án: 30

Kẻ đường kính AD của đường tròn ngoại tiếp $Δ ABC$ nên $\hat{ABD} = \hat{ACD} = 90^{°}$ .

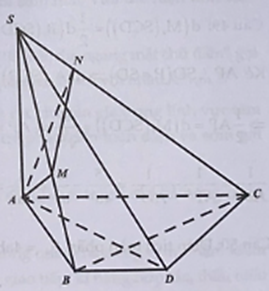
Cho hình chóp S.ABC có SA vuông góc với đáy, SA = 2BC và góc BAC = 120 độ. Hình chiếu vuông góc của A lên các đoạn SB và SC lần lượt là M và N. (ảnh 1)

Ta có $\{\begin{array}{l} B D ⊥ B A \\ B D ⊥ S A \end{array} \Rightarrow B D ⊥ (S A B)$ hay $B D ⊥ A M$ và $AM ⊥ SB$ hay $AM ⊥ (SBD) \Rightarrow AM ⊥ SD$ .

Chứng minh tương tự ta được $AN ⊥ SD$ .

Suy ra $SD ⊥ (AMN)$ , mà $SA ⊥ (ABC) \Rightarrow ((ABC), (AMN)) = (SA, SD) = \hat{DSA}$ .

Ta có $B C = 2 R \sin A = A D \cdot \frac{\sqrt{3}}{2} \Rightarrow S A = 2 B C = A D \sqrt{3}$ .

Vậy

\tan \hat{ASD} = \frac{AD}{SA} = \frac{1}{\sqrt{3}} \Rightarrow \hat{ASD} = 30^{°}

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong sân vận động có tất cả 30 dãy ghế, dãy đầu tiên có 15 ghế, các dãy liền sau nhiều hơn dãy trước 4 ghế, hỏi sân vận động đó có tất cả bao nhiêu ghế?

A. 2250.

B. 1740.

C. 4380.

D. 2190.

Lời giải

Chọn D

Gọi $u_{1}, u_{2}, \dots, u_{30}$ lần lượt là số ghế của dãy ghế thứ nhất, dãy ghế thứ hai,... và dãy ghế số ba mươi. Ta có công thức truy hồi ta có $u_{n} = u_{n - 1} + 4 (n = 2; 3; \dots; 30); u_{1} = 15$ .

Kí hiệu: $S_{30} = u_{1} + u_{2} + \dots + u_{30}$ , theo công thức tổng các số hạng của một cấp số cộng, ta được:

S_{30} = \frac{30}{2} (2 u_{1} + (30 - 1) 4) = 15 (2.15 + 29.4) = 2190

Câu 2

Một trang trại mỗi ngày thu hoạch được một tấn rau. Mỗi ngày, nếu bán rau với giá 30.000 đồng/kg thì hết sạch rau, nếu giá bán cứ tăng thêm 1000 đồng/kg thì số rau thừa lại tăng thêm 20 kg. Số rau thừa này được thu mua làm thức ăn chăn nuôi với giá 2000 đồng/kg. Hỏi số tiền bán rau nhiều nhất mà trang trại có thể thu lời một ngày là bao nhiêu?

Xem đáp án

Lời giải

Đáp số: 32420000

Gọi số tiền cần tăng giá mỗi kg rau là x (nghìn đồng).

Vì cứ tăng giá thêm 1000 đồng/kg thì số rau thừa lại 20kg nên tăng x (nghìn đồng) thì số rau thừa lại 20x kg. Do đó tổng số rau bán ra mỗi ngày là: 1000 - 20x kg. Do đó lợi nhuận một ngày là: $f (x) = (1000 - 20 x) (30 + x) + 20 x .2$ (nghìn đồng).

Xét hàm số $f (x) = (1000 - 20 x) (30 + x) + 20 x .2$ trên $(0; + \infty)$ .

Ta có: $f (x) = - 20 x^{2} + 440 x + 30000$

Hàm số đạt giá trị lớn nhất tại $x = - \frac{b}{2 a} = - \frac{440}{2 \cdot (- 20)} = 11$

Khi đó

\max_{x \in (0; + \infty)} f (x) = f (11) = 32420

(nghìn đồng) = 32.420.000 đồng.

Câu 3

Trong không gian Oxyz cho ba điểm A(1;1;1), B(5;-1;2), C(3;2;−4). Tìm tọa độ điểm M thỏa mãn $\vec{MA} + 2 \vec{MB} - \vec{MC} = \vec{0}$

A. $M (4; - \frac{3}{2}; \frac{9}{2})$

B. $M (4; - \frac{3}{2}; - \frac{9}{2})$

C. $M (4; \frac{3}{2}; \frac{9}{2})$

D. $M (- 4; - \frac{3}{2}; \frac{9}{2})$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Thắng lợi của phong trào “Đồng khởi” (1959 - 1960) tác động như thế nào đến sự phát triển của cách mạng miền Nam Việt Nam?

A. Chuyển cách mạng từ thế giữ gìn lực lượng sang thế tiến công.

B. Làm cho chính sách thực dân mới của Mĩ bị thất bại hoàn toàn.

C. Làm sụp đổ hoàn toàn chính quyền tay sai Ngô Đình Diệm.

D. Khiến Mĩ phải ngừng hẳn các hoạt động chống phá miền Nam.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong hệ tọa độ Oxy, cho ba điểm A(1;0), B(0;3) và C(-3;-5). Tìm điểm M thuộc trục hoành sao cho biểu thức $P = | 2 \vec{MA} - 3 \vec{MB} + 2 \vec{MC} |$ đạt giá trị nhỏ nhất.

A. M(4;0)

B. M(-4;0)

C. M(16;0)

D. M(-16;0)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Đọc đoạn trích sau đây và trả lời câu hỏi:

Một dân tộc đã gan góc chống ách nô lệ của Pháp hơn 80 năm nay, một dân tộc đã gan góc đứng về phe Đồng minh chống phát xít mấy năm nay, dân tộc đó phải được tự do! Dân tộc đó phải được độc lập!

Vì những lẽ trên, chúng tôi, Chính phủ lâm thời của nước Việt Nam Dân chủ Cộng hòa, trịnh trọng tuyên bố với thế giới rằng:

Nước Việt Nam có quyền hưởng tự do và độc lập, và sự thật đã thành một nước tự do, độc lập. Toàn thể dân tộc Việt Nam quyết đem tất cả tinh thần và lực lượng, tính mạng và của cải để giữ quyền tự do, độc lập ấy.

(Tuyên ngôn độc lập – Hồ Chí Minh)

Phong cách ngôn ngữ chính của đoạn trích trên là gì?

A. Phong cách ngôn ngữ hành chính

B. Phong cách ngôn ngữ nghệ thuật

C. Phong cách ngôn ngữ khoa học

D. Phong cách ngôn ngữ chính luận

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho ba số thực dương a, b, c đều khác 1 thỏa mãn $\log_{a} b = 2 \log_{b} c = 4 \log_{c} a$ và a + 2b + 3c = 48. Tính S = a + b + c.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Cho hình chóp S.ABC có SA vuông góc với đáy, SA = 2BC và góc BAC^=120°. Hình chiếu vuông góc của A lên các đoạn SB và SC lần lượt là M và N. Tính góc giữa hai mặt phẳng (ABC) và (AMN).

Trong sân vận động có tất cả 30 dãy ghế, dãy đầu tiên có 15 ghế, các dãy liền sau nhiều hơn dãy trước 4 ghế, hỏi sân vận động đó có tất cả bao nhiêu ghế?

Trong không gian Oxyz cho ba điểm A(1;1;1), B(5;-1;2), C(3;2;−4). Tìm tọa độ điểm M thỏa mãn MA→+2MB→−MC→=0→

Thắng lợi của phong trào “Đồng khởi” (1959 - 1960) tác động như thế nào đến sự phát triển của cách mạng miền Nam Việt Nam?

Trong hệ tọa độ Oxy, cho ba điểm A(1;0), B(0;3) và C(-3;-5). Tìm điểm M thuộc trục hoành sao cho biểu thức P=|2MA→−3MB→+2MC→| đạt giá trị nhỏ nhất.

Cho ba số thực dương a, b, c đều khác 1 thỏa mãn logab=2logbc=4logca và a + 2b + 3c = 48. Tính S = a + b + c.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình chóp S.ABC có SA vuông góc với đáy, SA = 2BC và góc $\hat{B A C} = 120^{°}$ . Hình chiếu vuông góc của A lên các đoạn SB và SC lần lượt là M và N. Tính góc giữa hai mặt phẳng (ABC) và (AMN).

Trong không gian Oxyz cho ba điểm A(1;1;1), B(5;-1;2), C(3;2;−4). Tìm tọa độ điểm M thỏa mãn $\vec{MA} + 2 \vec{MB} - \vec{MC} = \vec{0}$

Trong hệ tọa độ Oxy, cho ba điểm A(1;0), B(0;3) và C(-3;-5). Tìm điểm M thuộc trục hoành sao cho biểu thức $P = | 2 \vec{MA} - 3 \vec{MB} + 2 \vec{MC} |$ đạt giá trị nhỏ nhất.

Cho ba số thực dương a, b, c đều khác 1 thỏa mãn $\log_{a} b = 2 \log_{b} c = 4 \log_{c} a$ và a + 2b + 3c = 48. Tính S = a + b + c.