Câu hỏi:

11/07/2024 1,240

Cho hình chóp tứ giác đều cạnh đáy bằng a, SB = 2a. Tính thể tích khối cầu ngoại tiếp hình chóp?

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

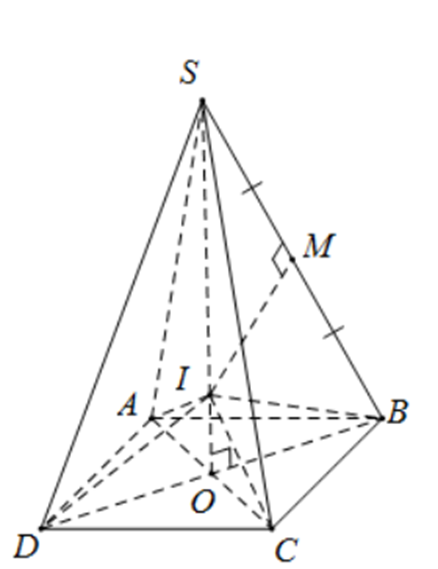
Cho hình chóp tứ giác đều cạnh đáy bằng a, SB = 2a. Tính thể tích khối cầu ngoại tiếp (ảnh 1)

Vì S.ABCD là hình chóp đều nên đường cao SO của hình chóp cũng chính là trục của đa giác đáy

Xét ΔBCD vuông cân tại C có BC = CD = a

⇒ BD = \(\sqrt {B{C^2} + C{D^2}} = a\sqrt 2 \)

⇒ BO = \(\frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}\)

Xét ΔSOB vuông tại O có SB = 2a , BO = \(\frac{{a\sqrt 2 }}{2}\)

⇒ SO = \(\sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt {14} }}{2}\)

Trong mặt phẳng (SOB), ta vẽ trung trực của SB, đường này cắt SO tại I. Rõ ràng I là tâm mặt cầu ngoại tiếp S.ABCD

Gọi M là trung điểm của SB

⇒ SM = \(\frac{1}{2}SB = a\)

Xét ΔSMI và ΔSOB ta có:

Chung \(\widehat S\)

\(\widehat {SMI} = \widehat {SOB} = 90^\circ \)

⇒ ΔSMI ~ΔSOB (g.g)

⇒ \(\frac{{SI}}{{SB}} = \frac{{SM}}{{SO}}\)

⇒ SI = \(\frac{{SB.SM}}{{SO}} = \frac{{2a.a}}{{\frac{{a\sqrt {14} }}{2}}} = \frac{{2a\sqrt {14} }}{7}\)

Vì SI chính là bán kính mặt cầu ngoại tiếp S.ABCD nên ta có:

V_{khối cầu} = \(\frac{4}{3}\)π.SI³ = \(\frac{{64\pi \sqrt {14} }}{{147}}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong một kì thi có 60% thí sinh thi đỗ. Hai bạn A và B cùng dự thi đó. Xác suất để chỉ có 1 bạn thi đỗ?

Xem đáp án

Lời giải

Gọi A là biến cố: “bạn A thi đỗ”, B là biến cố: “bạn B thi đỗ”, C là biến cố: “chỉ có một bạn thi đỗ”.

* Trường hợp 1: A thi đỗ, B thi không đỗ.

\(P\left( {A.\overline B } \right) = P\left( A \right).P\left( {\overline B } \right)\)= 0,6 . 0,4 = 0,24.

* Trường hợp 2: A thi không đỗ, B thi đỗ.

\(P\left( {\overline A .B} \right) = P\left( {\overline A } \right).P\left( B \right)\) = 0,4 . 0,6 = 0,24.

Theo quy tắc cộng xác suất, ta có

P(C) = \(P\left( {A.\overline B } \right) + P\left( {\overline A .B} \right)\)= 0,24 + 0,24 = 0,48.

Câu 2

Một ô tô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy với vận tốc 35km/h thì đến nơi chậm mất 2 giờ. Nếu xe chạy với vận tốc 50km/h thì đến nơi sớm hơn 1 giờ. Tìm quãng đường AB và thời gian dự định đi lúc đầu.

Xem đáp án

Lời giải

Gọi x (km) là độ dài quãng đường AB,

y (giờ) là thời gian dự định đi đến B lúc đầu. (x > 0, y > 1)

Thời gian đi từ A đến B với vận tốc 35km là:

\(\frac{x}{{35}}\) = y + 2 ⇒ x = 35.(y + 2) (1)

Thời gian đi từ A và B với vận tốc 50km là: \(\frac{x}{{50}}\) = y − 1 ⇒ x = 50.(y − 1) (2)

Từ (1) và (2) ta có:

35.(y + 2) = 50.(y − 1)

⇒ 35y + 70 = 50y – 50

⇒ y = 8

⇒ x = 35.(y + 2) = 35.10 = 350 (km)

Vậy quãng đường AB là 350km và thời gian dự định đi lúc đầu là 8 giờ.

Câu 3