Câu hỏi:
12/07/2024 2,752
Cho tam giác ABC. Gọi M là trung điểm của AB và N là điểm trên cạnh AC sao cho NC = 2NA. Gọi K là trung điểm của MN. Biểu diễn \(\overrightarrow {AK} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \).
Cho tam giác ABC. Gọi M là trung điểm của AB và N là điểm trên cạnh AC sao cho NC = 2NA. Gọi K là trung điểm của MN. Biểu diễn \(\overrightarrow {AK} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \).
Quảng cáo
Trả lời:
Giải bởi Vietjack
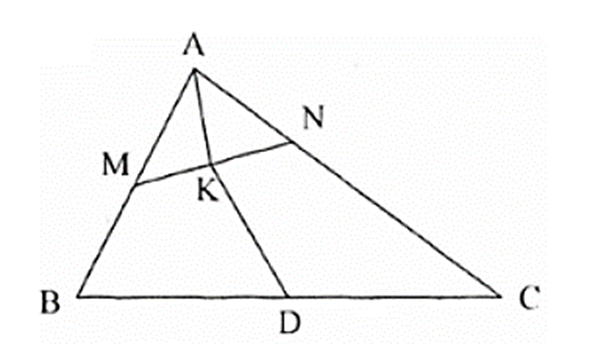
Do M là trung điểm AB nên \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} \)
Vì NC = 2NA nên \(\overrightarrow {AN} = \frac{1}{3}\overrightarrow {AC} \)
Ta có: \[\overrightarrow {AK} = \frac{1}{2}\left( {\overrightarrow {AM} + \overrightarrow {AN} } \right)\](Vì K là trung điểm MN)
\[ = \frac{1}{2}.\left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right)\]
\[ = \frac{1}{4}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi A là biến cố: “bạn A thi đỗ”, B là biến cố: “bạn B thi đỗ”, C là biến cố: “chỉ có một bạn thi đỗ”.
* Trường hợp 1: A thi đỗ, B thi không đỗ.
\(P\left( {A.\overline B } \right) = P\left( A \right).P\left( {\overline B } \right)\)= 0,6 . 0,4 = 0,24.
* Trường hợp 2: A thi không đỗ, B thi đỗ.
\(P\left( {\overline A .B} \right) = P\left( {\overline A } \right).P\left( B \right)\) = 0,4 . 0,6 = 0,24.
Theo quy tắc cộng xác suất, ta có
P(C) = \(P\left( {A.\overline B } \right) + P\left( {\overline A .B} \right)\)= 0,24 + 0,24 = 0,48.
Lời giải
Gọi x (km) là độ dài quãng đường AB,
y (giờ) là thời gian dự định đi đến B lúc đầu. (x > 0, y > 1)
Thời gian đi từ A đến B với vận tốc 35km là:
\(\frac{x}{{35}}\) = y + 2 ⇒ x = 35.(y + 2) (1)
Thời gian đi từ A và B với vận tốc 50km là: \(\frac{x}{{50}}\) = y − 1 ⇒ x = 50.(y − 1) (2)
Từ (1) và (2) ta có:
35.(y + 2) = 50.(y − 1)
⇒ 35y + 70 = 50y – 50
⇒ y = 8
⇒ x = 35.(y + 2) = 35.10 = 350 (km)
Vậy quãng đường AB là 350km và thời gian dự định đi lúc đầu là 8 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo