Cho (O) đường kính AC . trên đoạn OC lấy điểm B và vẽ đường tròn tâm O', đường kính BC. Gọi M là trung điểm của đoạn AB . Từ M vẽ dây cung DE vuông góc với AB, DC cắt đường tròn tâm O' tại I.
1. Tứ giác ADBE là hình gì?
2. Chứng minh DMBI nội tiếp.
3. Chứng minh B, I ,E Thẳng hàng và MI = MD.
4. Chứng minh MC.DB = MI.DC.
5. Chứng minh MI là tiếp tuyến của (O').
Cho (O) đường kính AC . trên đoạn OC lấy điểm B và vẽ đường tròn tâm O', đường kính BC. Gọi M là trung điểm của đoạn AB . Từ M vẽ dây cung DE vuông góc với AB, DC cắt đường tròn tâm O' tại I.
1. Tứ giác ADBE là hình gì?
2. Chứng minh DMBI nội tiếp.
3. Chứng minh B, I ,E Thẳng hàng và MI = MD.
4. Chứng minh MC.DB = MI.DC.
5. Chứng minh MI là tiếp tuyến của (O').
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
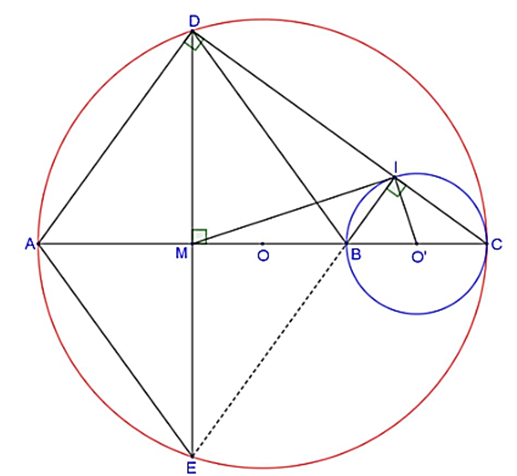
1) Ta có OM ⊥ DE tại M
Nên M là trung điểm của DE(quan hệ đường kính – dây cung)
Xét tứ giác ADBE, ta có:
M là trung điểm của AB(gt)
M là trung điểm của DE(cmt)
AB ⊥ DE tại M (gt)
Nên tứ giác ADBE là hình thoi
2) Ta có: \(\widehat {BIC} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Vậy tứ giác DMBI có \(\widehat {DMB} = \widehat {BIC} = 90^\circ \)
Nên DMBI nội tiếp (góc ngoài bằng góc đối trong)
3) Ta có \(\widehat {ADC} = \widehat {BIC} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Nên AD ⊥ DC và BI ⊥ DC
⇒ AD // BI
Mà AD // BE (vì ADBE là hình thoi)
Do đó BI ≡ BE ⇒ B, I, E thẳng hàng
Vậy ΔDIEvuông tại I có IM là đường trung tuyến nên MI = MD
4) Vì DMBI nội tiếp nên \(\widehat {BMI} = \widehat {BDI}\)(cùng chắn cung BI)
Xét ΔMICΔ và ΔDBC, ta có:
\(\widehat {BMI} = \widehat {BDI}\)
\(\widehat {MCI}\)là góc chung
Nên ΔMIC ~ ΔDBC(g.g)
⇒ \(\frac{{MI}}{{DB}} = \frac{{MC}}{{DC}}\)
⇒ MC.DB = MI.DC
5) Ta có:
\[\widehat {MIB} = \widehat {MDB}\](vì DMBI nội tiếp)
\[\widehat {MDA} = \widehat {MDB}\](vì ADBE là hình thoi)
\[\widehat {MDA} = \widehat {BCI}\] (cùng phụ \(\widehat {DAM}\))
(trong (O′)
Nên (trong (O′)
Vậy MI là tiếp tuyến của (O′).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi A là biến cố: “bạn A thi đỗ”, B là biến cố: “bạn B thi đỗ”, C là biến cố: “chỉ có một bạn thi đỗ”.
* Trường hợp 1: A thi đỗ, B thi không đỗ.
\(P\left( {A.\overline B } \right) = P\left( A \right).P\left( {\overline B } \right)\)= 0,6 . 0,4 = 0,24.
* Trường hợp 2: A thi không đỗ, B thi đỗ.
\(P\left( {\overline A .B} \right) = P\left( {\overline A } \right).P\left( B \right)\) = 0,4 . 0,6 = 0,24.
Theo quy tắc cộng xác suất, ta có
P(C) = \(P\left( {A.\overline B } \right) + P\left( {\overline A .B} \right)\)= 0,24 + 0,24 = 0,48.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi x (km) là độ dài quãng đường AB,
y (giờ) là thời gian dự định đi đến B lúc đầu. (x > 0, y > 1)
Thời gian đi từ A đến B với vận tốc 35km là:
\(\frac{x}{{35}}\) = y + 2 ⇒ x = 35.(y + 2) (1)
Thời gian đi từ A và B với vận tốc 50km là: \(\frac{x}{{50}}\) = y − 1 ⇒ x = 50.(y − 1) (2)
Từ (1) và (2) ta có:
35.(y + 2) = 50.(y − 1)
⇒ 35y + 70 = 50y – 50
⇒ y = 8
⇒ x = 35.(y + 2) = 35.10 = 350 (km)
Vậy quãng đường AB là 350km và thời gian dự định đi lúc đầu là 8 giờ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập