Câu hỏi:

12/07/2024 2,683

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với $A B = a, A D = a \sqrt{3}$ . Hình chiếu vuông góc H của S lên mặt đáy trùng với trọng tâm của tam giác ABC và $S H = \frac{a}{2}$ . Gọi M, N lần lượt là trung điểm của các cạnh BC, SC. Tính tan của góc giữa đường thẳng MN và mặt phẳng (ABCD)? (Kết quả làm tròn đến hàng phần trăm.)

Xem lời giải

Câu hỏi trong đề: Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 8) !!

Bắt đầu thi

Trả lời:

Giải bởi Vietjack

Đáp án: 0,75

Qua N kẻ đường thẳng song song với SH cắt CH tại $K \Rightarrow NK ⊥ (ABCD)$ .

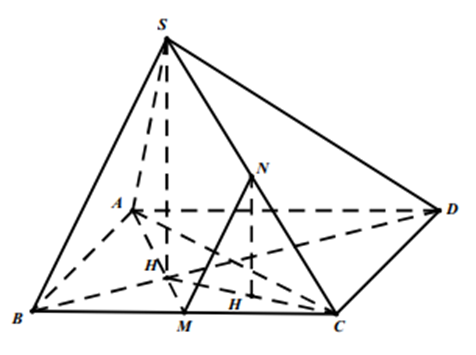
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với ab = a, ad = a căn 3. Hình chiếu vuông góc H của S lên mặt đáy trùng với trọng tâm của tam giác ABC và sh = a/2 (ảnh 1)

Ta có $MN \cap (ABCD) = {M}$ và $NK ⊥ (ABCD) \Rightarrow \hat{(MN, (ABCD))} = \hat{MN, MK} = \hat{KMN}$

Ta có $NK = \frac{1}{2} SH = \frac{a}{4}$ . Ta có $BH = \frac{1}{3} BH = \frac{2 a}{3}$

$\Rightarrow SB = \sqrt{{SH}^{2} + {HB}^{2}} = \frac{5 a}{6} \Rightarrow MN = \frac{1}{2} SB = \frac{5 a}{12} \Rightarrow MK = \sqrt{{MN}^{2} - {NK}^{2}} = \frac{a}{3} \Rightarrow \tan \hat{KMN} = \frac{NK}{MK} = \frac{3}{4}$

Bình luận

Câu 1:

Anh Phong có một cái ao với diện tích 50 m² để nuôi cá diêu hồng. Vụ vừa qua, anh nuôi với mật độ 20 con/m² và thu được 1,5 tấn cá thành phẩm. Theo kinh nghiệm nuôi cá của mình anh thấy cứ thả giảm đi 8 con/m² thì mỗi con cá thành phẩm thu được tăng thêm 0,5 kg. Hỏi để tổng năng suất cao nhất thì vụ tới anh nên mua bao nhiêu cá giống để thả? (giả sử không có hao hụt trong quá trình nuôi).

Xem đáp án » 12/07/2024 45,230

Câu 2:

Một xưởng sản xuất thực phẩm gồm 4 kỹ sư chế biến thực phẩm, 3 kỹ thuật viên và 13 công nhân. Để đảm bảo sản xuất thực phẩm chống dịch Covid-19, xưởng cần chia thành 3 ca sản xuất theo thời gian liên tiếp nhau sao cho ca 1có 6 người và 2 ca còn lại mỗi ca có 7 người. Tính xác suất sao cho mỗi ca có 1 kĩ thuật viên, ít nhất một kĩ sư chế biến thực phẩm

A. $\frac{440}{3320}$

B. $\frac{441}{3230}$

C. $\frac{41}{230}$

D. $\frac{401}{3320}$

Xem đáp án » 12/08/2023 6,048

Câu 3:

Một nhà máy thủy điện xả lũ với tốc độ xả tại thời điểm t giây là v(t) = 2t + 100 (m³/s). Hỏi sau 30 phút nhà máy xả được bao nhiêu mét khối nước?

A. 3.240.000.

B. 3.420.000.

C. 4.320.000.

D. 4.230.000.

Xem đáp án » 12/08/2023 3,079

Câu 4:

Khu vực Đông Nam Á nằm ở

A. phía đông nam châu Á.

B. giáp với Đại Tây Dương.

C. giáp lục địa Ô-xtrây-li-a.

D. phía bắc nước Nhật Bản.

Xem đáp án » 12/08/2023 2,751

Câu 5:

Biểu đồ dưới đây là phổ điểm lịch sử vào 10 năm 2020.

Tỉ lệ % học sinh đạt trên 8 điểm gần nhất với đáp án nào dưới đây?

A. 45%.

B. 40,2%.

C. 38,36%.

D. 35,36%.

Xem đáp án » 12/08/2023 2,729

Câu 6:

Cho f(x) là hàm số liên tục trên tập số thực R và thỏa mãn $f (x^{2} + 3 x + 1) = x + 2$ . Tính $I = \int_{1}^{5} f (x) d x$

A. $\frac{37}{6}$

B. $\frac{529}{3}$

C. $\frac{61}{6}$

D. $\frac{464}{3}$

Xem đáp án » 12/08/2023 2,507

Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1)

Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn)

Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1)

Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn)

Bình luận

Một nhà máy thủy điện xả lũ với tốc độ xả tại thời điểm t giây là v(t) = 2t + 100 (m³/s). Hỏi sau 30 phút nhà máy xả được bao nhiêu mét khối nước?

Khu vực Đông Nam Á nằm ở

Biểu đồ dưới đây là phổ điểm lịch sử vào 10 năm 2020.

Tỉ lệ % học sinh đạt trên 8 điểm gần nhất với đáp án nào dưới đây?

Cho f(x) là hàm số liên tục trên tập số thực R và thỏa mãn $f (x^{2} + 3 x + 1) = x + 2$ . Tính $I = \int_{1}^{5} f (x) d x$

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

Bình luận

Một nhà máy thủy điện xả lũ với tốc độ xả tại thời điểm t giây là v(t) = 2t + 100 (m3/s). Hỏi sau 30 phút nhà máy xả được bao nhiêu mét khối nước?

Khu vực Đông Nam Á nằm ở

Biểu đồ dưới đây là phổ điểm lịch sử vào 10 năm 2020. Tỉ lệ % học sinh đạt trên 8 điểm gần nhất với đáp án nào dưới đây?

Cho f(x) là hàm số liên tục trên tập số thực R và thỏa mãn fx2+3x+1=x+2. Tính I=∫15f(x)dx

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Một nhà máy thủy điện xả lũ với tốc độ xả tại thời điểm t giây là v(t) = 2t + 100 (m³/s). Hỏi sau 30 phút nhà máy xả được bao nhiêu mét khối nước?

Biểu đồ dưới đây là phổ điểm lịch sử vào 10 năm 2020.

Tỉ lệ % học sinh đạt trên 8 điểm gần nhất với đáp án nào dưới đây?

Cho f(x) là hàm số liên tục trên tập số thực R và thỏa mãn $f (x^{2} + 3 x + 1) = x + 2$ . Tính $I = \int_{1}^{5} f (x) d x$