Câu hỏi:
13/07/2024 735
Tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số:
y = ∣3x4 + 8x3 − 6x2 − 24x − m∣ có 7 điểm cực trị.
Tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số:
y = ∣3x4 + 8x3 − 6x2 − 24x − m∣ có 7 điểm cực trị.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét hàm số: y = 3x4 + 8x3 − 6x2 − 24x – m
Ta có: y’ = 12x3 + 24x2 – 1x – 24 = 0
\[ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\\x = - 2\end{array} \right.\]
Bảng biến thiên:
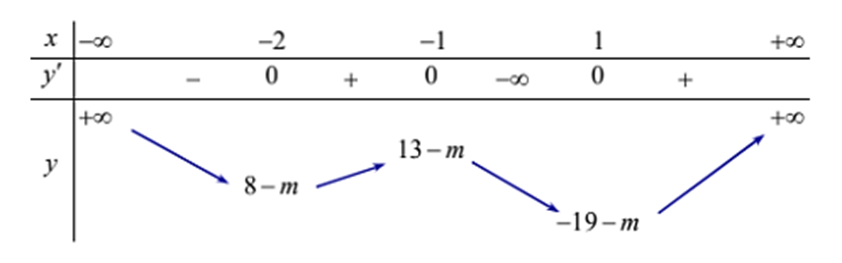
Dựa vào bảng biến thiên ta thấy để đồ thị hàm số y = ∣3x4 + 8x3 − 6x2 − 24x − m∣ có 7 điểm cực trị.
\[ \Leftrightarrow \left[ \begin{array}{l}8 - m < 0\\13 - m > 0\end{array} \right. \Leftrightarrow 8 < m < 13\]
\[ \Rightarrow m \in \left\{ {9;\,\,10;\,\,11;\,\,12} \right\}\].
Tổng tất cả các giá trị của m thỏa mãn bài toán là: 9 + 10 + 11 + 12 = 42.
Vậy tổng các giá trị m thoả mãn là 42.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(sin2 x)’ = 2sin x.(sin x)’ = 2sin x cos x = sin 2x.
Vậy đạo hàm của hàm số sin2 x là sin 2x.
Lời giải
Ta có: cosx ∈ [−1; 1]
Để phương trình có nghiệm thì:
− 1 ≤ m − 1 ≤ 1 suy ra 0 ≤ m ≤ 2
Vậy m ∈ [0; 2].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)