Câu hỏi:
15/08/2023 27,657
Gọi S là tập hợp các số tự nhiên có hai chữ số. Chọn ngẫu nhiên đồng thời hai số từ tập hợp S. tính xác suất để hai số được chọn có chữ số hàng đơn vị giống nhau.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Số tự nhiên có 2 chữ số là: \(C_9^1.C_{10}^1 = 90\) (số).
\(\Omega :\) “Chọn ngẫu nhiên 2 số từ tập hợp S” ⇒ \({n_\Omega } = C_{90}^2\)
A: “Chọn được 2 số có chữ số hàng đơn vị giống nhau”.
· TH1: Chữ số hàng đơn vị là 0 ⇒ Có 9 chữ số là: 10; 20; 30; 40; 50; 60; 70; 80; 90.
⇒ Số cách chọn 2 số là: \(C_9^2.\)
Tương tự với các số có chữ số hàng đơn vị là: 1; 2; 3; 4; 5; 6; 7; 8; 9.
⇒ Có tất cả 10 trường hợp giống nhau.
⇒ \({n_A} = 10.C_9^2\)
⇒ \({P_A} = \frac{{10.C_9^2}}{{C_{90}^2}} = \frac{8}{{89}}.\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Có tất cả 5 + 4 + 3 = 12 quyển sách.
Cách sắp xếp các quyển sách một cách tùy ý là: 12! (cách)
b) Chọn vị trí ở giữa cho 5 quyển sách Toán nên có số cách là 5! (cách)
Chọn vị trí đầu cho sách lý, có số cách là 4! (cách)
Chọn vị trí cuối cho sách văn, có số cách là 3! (cách)
Hoán đổi vị trí đầu và vị trí cuối nên thêm 2! (cách)
Vậy số cách sắp xếp các quyển sách trên theo từng môn và sách Toán nằm ở giữa là:
4!.5!.3!.2! = 34560 (cách)
Lời giải
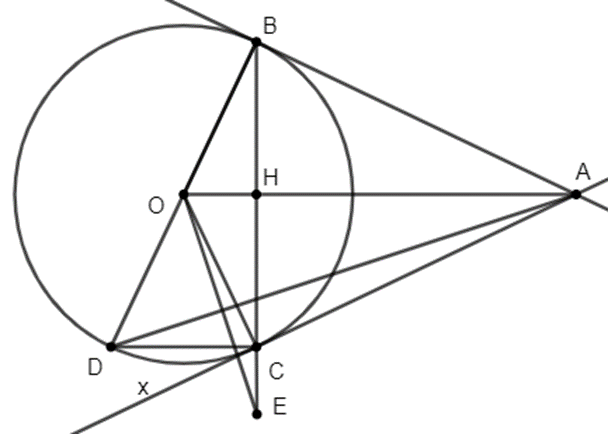
a) Vì AB, AC là tiếp tuyến của (O) nên \(\widehat {ABO} = \widehat {ACO} = 90^\circ \)
Xét tứ giác ABOC có: \(\widehat {ABO} + \widehat {ACO} = 90^\circ + 90^\circ = 180^\circ \)
⇒ Tứ giác ABOC nội tiếp ⇒ A, B, O, C cùng thuộc đường tròn đường kính OA.
Vì AB, AC là tiếp tuyến của (O) nênAO là đường trung trực của BC.
Do đó AO ⊥ BC tại H.
b) Xét ∆BCD có: H là trung điểm của BC, O là trung điểm của BD
Suy ra OH là đường trung bình của ∆BCD.
Do đó OH // CD hay OA // CD.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận