Câu hỏi:
18/08/2023 4,541
Một vận động viên bắn súng, bắn ba viên đạn. Xác suất để trúng cả ba viên vòng 10 là 0,0008; xác suất đề một viên trúng vòng 8 là 0,15; xác suất để một viên trúng vòng dưới 8 là 0,4. Biết rằng các lần bắn là độc lập với nhau. Xác suất để vận động viên đó đạt ít nhất 28 điểm có giá trị gần bằng nhất với số nào sau đây?
Một vận động viên bắn súng, bắn ba viên đạn. Xác suất để trúng cả ba viên vòng 10 là 0,0008; xác suất đề một viên trúng vòng 8 là 0,15; xác suất để một viên trúng vòng dưới 8 là 0,4. Biết rằng các lần bắn là độc lập với nhau. Xác suất để vận động viên đó đạt ít nhất 28 điểm có giá trị gần bằng nhất với số nào sau đây?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Xác suất để một viên trúng vòng 10 là \(\sqrt[3]{{0,0008}} \approx 0,0928.\)
Xác suất để một viên trúng vòng 9 là 1 − 0,4 − 0,0928 − 0,15 = 0,3572.
Các trường hờp xảy ra để thỏa mãn yêu cầu bài toán:
· Điểm ba lần bắn là 28 điểm, có 2 trường hợp: hai viên vòng 9 và một viên vòng 10 hoặc hai viên vòng 10 và một viên vòng 8 .
Xác suất trong trường hợp này bằng:
\({P_1} = C_3^2.{\left( {0,3572} \right)^2}.0,0928 + C_3^2.{\left( {0,0928} \right)^2}.0,15 \approx 0,0394.\)
· Điểm ba lần bắn là 29 điểm, có 1 trường hợp: hai viên vòng 10 và một viên vòng 9.
Xác suất trường hợp này bằng:
\({P_2} = C_3^2.{\left( {0,0928} \right)^2}.0,3572 \approx 0,0092.\)
· Điểm ba lần bắn là 30 điểm, có 1 trường hợp là cả ba viên vòng 10 : xác suất bằng 0,0008.
Vậy xác suất cần tìm bằng: P1 + P2 + 0,0008 = 0,0494.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
ĐK: x > 0.
\(\log _2^2x - 2{\log _2}\left( {2x} \right) - 1 = 0\) ⇔ \(\log _2^2x - 2{\log _2}2 - 2{\log _2}x - 1 = 0\)
⇔ \(\log _2^2x - 2{\log _2}x - 3 = 0\) (*)
Đặt log2x = t. Khi đó ta có:
(*) ⇔ \({t^2} - 2t - 3 = 0\) ⇔ (t + 1)(t – 3) = 0
⇔ \(\left[ {\begin{array}{*{20}{c}}{t + 1 = 0}\\{t - 3 = 0}\end{array}} \right.\) ⇔ \(\left[ {\begin{array}{*{20}{c}}{t = - 1}\\{t = 3}\end{array}} \right.\) ⇔ \(\left[ {\begin{array}{*{20}{c}}{{{\log }_2}x = - 1}\\{{{\log }_2}x = 3}\end{array}} \right.\)
⇔ \(\left[ {\begin{array}{*{20}{c}}{x = {2^{ - 1}} = \frac{1}{2}\left( {tm} \right)}\\{x = {2^3} = 8\left( {tm} \right)}\end{array}} \right.\)
⇒ \({x_1}{x_2} = \frac{1}{2}.8 = 4.\)
Lời giải
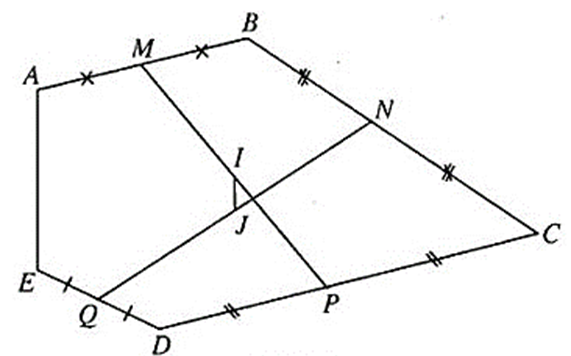
Ta có: \(2\overrightarrow {IJ} = \overrightarrow {IQ} + \overrightarrow {IN} = \overrightarrow {IM} + \overrightarrow {MQ} + \overrightarrow {IP} + \overrightarrow {PN} = \overrightarrow {MQ} + \overrightarrow {PN} \)
\( = \frac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {BD} } \right) + \frac{1}{2}\overrightarrow {DB} = \frac{1}{2}\overrightarrow {AE} \)
Do đó: \(\overrightarrow {IJ} = \frac{1}{4}\overrightarrow {AE} \) ⇒ \(4\overrightarrow {IJ} = \overrightarrow {AE} .\)
Vậy IJ // AE và 4IJ = AE.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)