Cho hàm số y = f(x) có đạo hàm . Có bao nhiêu giá trị nguyên của tham số m để hàm số có 5 điểm cực trị.
Câu hỏi trong đề: Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 14) !!
Quảng cáo
Trả lời:
Suy ra để g(x) có 5 điểm cực trị khi và chỉ khi mối phương trình và có hai nghiệm phân biệt khác 5
Vậy có 9 giá trị nguyên của m thỏa mãn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
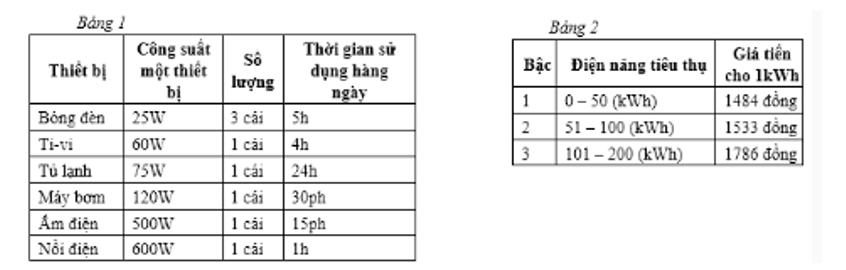
A. 150000 đồng.
B.138000 đồng.
D.145000 đồng.
Lời giải
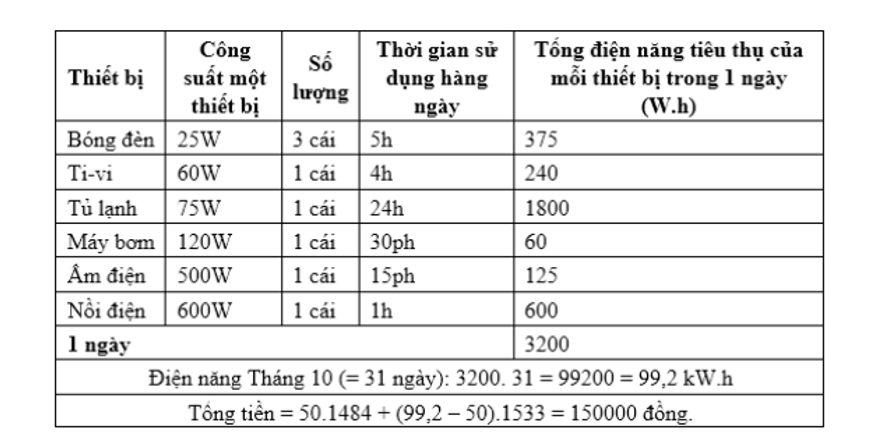
Lời giải
Hai vectơ cùng phương
Câu 3
A. Biểu cảm
B. Nghị luận
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Vì Xuân Diệu thường lấy vẻ đẹp của con người làm chuẩn mực cho mọi vẻ đẹp
B. Vì cảnh vật trong thơ Xuân Diệu luôn đầy sắc dục, tỉnh tử
C. Vì Xuân Diệu nhìn đâu cũng thấy niềm đam mê và hương vị của tỉnh yêu
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Sự ảm đạm, cô liêu của núi rừng Tây Bắc
B. Thiên nhiên bốn mùa ở Tây Bắc
C. Nỗi nhớ con sông Đà của tác giả
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.