Câu hỏi:
13/07/2024 12,814
Cho đường tròn (O;R) đường kính AB. Vẽ tiếp tuyến Bx của (O). Trên cùng 1 nửa mặt phẳng bờ AB có chứa Bx, lấy điểm M thuộc (O) (M khác A và B) sao cho MA > MB. Tia AM cắt Bx tại C. Từ C kẻ tiếp tuyến thứ hai CD với (O) (D là tiếp điểm)
a) Chứng minh OC ⊥ BD.
b) Chứng minh bốn điểm O, B, C, D cùng thuộc một đường tròn.
c) Chứng minh \(\widehat {CMD} = \widehat {CDA}\).
d) Kẻ MH vuông góc với AB tại H. Tìm vị trí của M để chu vi tam giác OMH đạt giá trị lớn nhất.
Cho đường tròn (O;R) đường kính AB. Vẽ tiếp tuyến Bx của (O). Trên cùng 1 nửa mặt phẳng bờ AB có chứa Bx, lấy điểm M thuộc (O) (M khác A và B) sao cho MA > MB. Tia AM cắt Bx tại C. Từ C kẻ tiếp tuyến thứ hai CD với (O) (D là tiếp điểm)
a) Chứng minh OC ⊥ BD.
b) Chứng minh bốn điểm O, B, C, D cùng thuộc một đường tròn.
c) Chứng minh \(\widehat {CMD} = \widehat {CDA}\).
d) Kẻ MH vuông góc với AB tại H. Tìm vị trí của M để chu vi tam giác OMH đạt giá trị lớn nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có : CD, CB là tiếp tuyến của (O) ⇒ CO ⊥ BD
b) Vì CD, CB là tiếp tuyến của (O) ⇒ CD ⊥ OD, CB ⊥ OB
⇒ O, B, C, D cùng thuộc đường tròn đường kính OC
c) Ta có : CD là tiếp tuyến của (O)
(góc nội tiếp cùng chắn cung DM)
Xét tam giác CDM và tam giác CAD có:
\(\widehat {CDM} = \widehat {CAD}\)
Chung \(\widehat C\)
⇒ ∆CDM ∽ ∆CAD (g.g)
⇒ \(\widehat {CMD} = \widehat {CDA}\)
d) Ta có :
POMH = OM + MH + HO = R + MH + HO
→Để POMH lớn nhất
→ MH + HO lớn nhất
Mà MH + HO = \(\sqrt {{{\left( {MH + HO} \right)}^2}} \le \sqrt {2\left( {M{H^2} + H{O^2}} \right)} = \sqrt {2{R^2}} = R\sqrt 2 \)
MH + HO lớn nhất khi MH = OH
Suy ra: \(\widehat {MOH} = 45^\circ \Rightarrow \widehat {MOB} = 45^\circ \).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
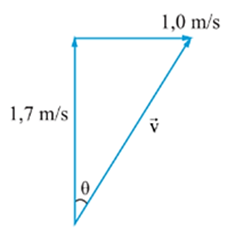
Độ lớn vận tốc tổng hợp của vận động viên là:
\(\overrightarrow v \)tổng hợp = \(\overrightarrow v \) + \(\overrightarrow v \)nước
Suy ra: vtổng hợp = \(\sqrt {{v^2} + {v_{nuoc}}^2} = \sqrt {1,{7^2} + {1^2}} = 1,97\left( {m/s} \right)\)
Hướng vận tốc tổng hợp của vận động viên hợp với bờ sông 1 góc là:
\(\tan \alpha = \frac{v}{{{v_{nuoc}}}} = \frac{{1,7}}{1} = 1,7 \Rightarrow \alpha \approx 59,53^\circ \)
Lời giải
y = f(x2 + 2x)
y' = (2x + 2)f'(x2 + 2x)
Xét y' = 0 ta có: (2x + 2)f'(x2 + 2x) = 0
⇒ \(\left[ \begin{array}{l}2x + 2 = 0\\f'\left( {{x^2} + 2x} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\{x^2} + 2x = - 2\\{x^2} + 2x = 1\\{x^2} + 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = - 3\\x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\)
Ta có bảng biến thiên:
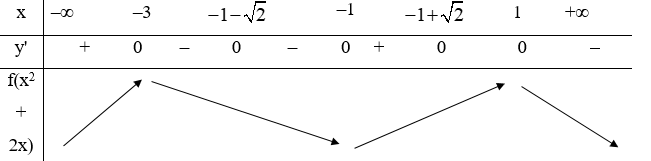
Vậy hàm số nghịch biến trên (–3; –1) và (1; +∞)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
Nhắn tin Zalo