Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD. Chứng minh rằng $\hat{S B C} = \hat{S C D} = 90 °$ .

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

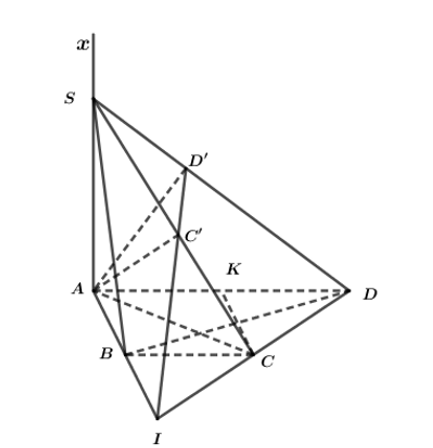
Ta có: SA ^ BC; AB ^ BC

Þ SB ^ BC (định lý 3 đường vuông góc) hay $\hat{S B C} = 90 °$ .

Gọi K là trung điểm của AD ta có CK = AB = AD/2 nên tam giác ACD vuông tại C

Ta có: CD ^ AC; CD ^ SA

Þ CD ^ (SAC)

Dó đó CD ^ SC hay $\hat{S C D} = 90 °$

Vậy $\hat{S B C} = \hat{S C D} = 90 °$

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xem đáp án

Lời giải

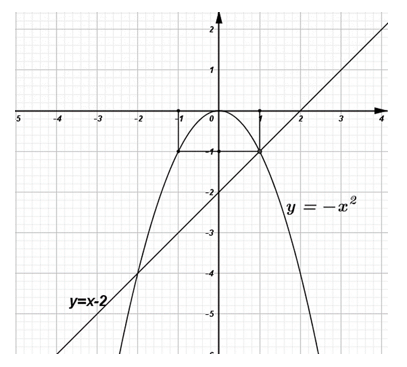
y = −x²

Với x = 0 ⇒ y = 0, với x = ±1 ⇒ y = −1

Đồ thị hàm số y = −x² có đỉnh là (0;0) và đi qua 2 điểm (1;−1) và (−1;−1)

y = x − 2

Với x = 0 ⇒ y = −2, với y = 0 ⇒ x = 2

Đồ thị hàm số y = x − 2 đi qua điểm (0;−2) và (2;0)

Đồ thị của hai hàm số như hình vẽ.

Câu 2

Xem đáp án

Lời giải

Xét phương trình:

f'(x) = x²(x − 1)(x + 2)²(x − 2) = 0

$\Leftrightarrow [\begin{array}{l} x = 0 \\ x = 1 \\ x = - 2 \\ x = 2 \end{array}$

Hàm số đã cho không đạt cực trị tại điểm x = 0 vì là nghiệm bội hai của phương trình f'(x) = 0.

Vậy hàm số đã cho có 3 điểm cực trị.

Câu 3