Quảng cáo
Trả lời:
Ta có: 5x2 + 16y2 + 27z2 − 12xy − 12xz − 12yz
= 3(x − 2y)2 + (2y − 3z)2 + 2(x − 3z)2 ≥ 0
Dấu đẳng thức xảy ra khi và chỉ khi x = 2y = 3z (1)
Suy ra 5x2 + 16y2 + 27z2 ≥ 12(xy + yz + xz)
(có xy + yz + xz ≥ 1 nên hàm số đồng biến)
Biểu thức đã cho:
Dấu đẳng thức xảy ra khi và chỉ khi
⇔ xy + yz + xz = 122 (2)
Từ (1), (2) suy ra đẳng thức đã cho xảy ra khi
Suy ra x + y – z = 14
Vậy x + y – z = 14.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
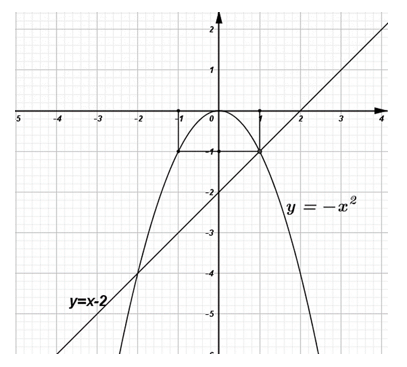
y = −x2
Với x = 0 ⇒ y = 0, với x = ±1 ⇒ y = −1
Đồ thị hàm số y = −x² có đỉnh là (0;0) và đi qua 2 điểm (1;−1) và (−1;−1)
y = x − 2
Với x = 0 ⇒ y = −2, với y = 0 ⇒ x = 2
Đồ thị hàm số y = x − 2 đi qua điểm (0;−2) và (2;0)
Đồ thị của hai hàm số như hình vẽ.
Lời giải
Xét phương trình:
f'(x) = x2(x − 1)(x + 2)2(x − 2) = 0
Hàm số đã cho không đạt cực trị tại điểm x = 0 vì là nghiệm bội hai của phương trình f'(x) = 0.
Vậy hàm số đã cho có 3 điểm cực trị.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.