Giá trị lớn nhất của biết thức F (x; y) = x + 2y với điều kiện $\left\{\begin{array}{l}0\le y\le 4\\ x\ge 0\\ x-y-1\le 0\\ x+2y-10\le 0\end{array}\right.$  là

• Vẽ đường thẳng d₁: x − y − 1 = 0, đường thẳng d₁ qua hai điểm (0; −1) và (1; 0).

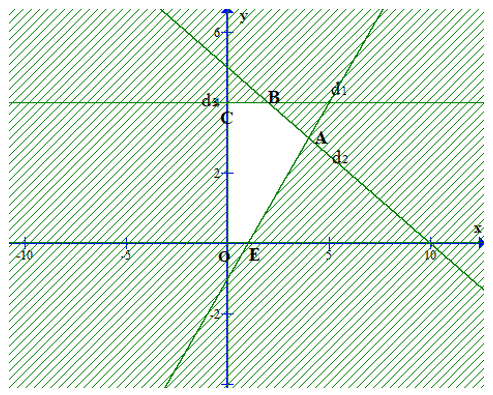
Xét điểm O(0; 0) thay vào phương trình đường thẳng, ta có 0 − 0 − 1 = −1 < 0.

Thoả mãn bất phương trình x − y − 1 ≤ 0.

Vậy O(0; 0) thuộc miền nghiệm của bất phương trình.

Do đó miền nghiệm D₁ là nửa mặt phẳng không bị gạch được chia bởi đường thẳng d₁ chứa gốc tọa độ O kể cả bờ.

• Vẽ đường thẳng d₂: x + 2y − 10 = 0, đường thẳng d₂ qua hai điểm (0; 5) và (10; 0).

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 + 2.0 − 10 = −10 < 0. Thoả mãn bất phương trình x + 2y − 10 ≤ 0.

Vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình.

Do đó miền nghiệm D₂ là nửa mặt phẳng không bị gạch được chia bởi đường thẳng d₂ chứa gốc tọa độ O kể cả bờ.

• Vẽ đường thẳng d₃: y = 4.

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 < 4.

Thoả mãn bất phương trình 0 ≤ y ≤ 4.

Vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình.

Do đó miền nghiệm D₃ là nửa mặt phẳng không bị gạch được chia bởi đường thẳng d₃ chứa gốc tọa độ O kể cả bờ.

x ≥ 0 có miền nghiệm là nửa mặt phẳng nằm bên phải trục tung (kể cả trục tung).

y ≥ 0 có miền nghiệm là nửa mặt phẳng nằm phía trên trục hoành (kể cả trục hoành).

Miền nghiệm là phần không bị gạch như hình vẽ.

Miền nghiệm là ngũ giác ABCOE với A(4; 3), B(2; 4), C(0; 4), O(0; 0), E(1; 0).

Nhận thấy biểu thức F (x; y) = x + 2y đạt giá trị lớn nhất tại các điểm A, B, C, O, E.

Do F (x; y) = x + 2y suy ra:

F(4; 3) = 4 + 2.3 = 10;

F(0; 4) = 0 + 2.4 = 8;

F(2; 4) = 2 + 2.4 = 10;

F(1; 0) = 1 + 2.0 = 1;

F(0; 0) = 0 + 2.0 = 0.

Vậy giá trị lớn nhất của biết thức F(x; y) = x + 2y bằng 10.