Một thầy giáo có 10 cuốn sách khác nhau trong đó có 4 cuốn sách Toán, 3 cuốn sách Lí, 3 cuốn sách Hóa. Thầy muốn lấy ra 5 cuốn và tặng cho 5 em học sinh A, B, C, D, E mỗi em một cuốn. Hỏi thầy giáo có bao nhiêu cách tặng cho các em học sinh sao cho sau khi tặng xong, mỗi một trong ba loại sách trên đều còn ít nhất một cuốn?
Một thầy giáo có 10 cuốn sách khác nhau trong đó có 4 cuốn sách Toán, 3 cuốn sách Lí, 3 cuốn sách Hóa. Thầy muốn lấy ra 5 cuốn và tặng cho 5 em học sinh A, B, C, D, E mỗi em một cuốn. Hỏi thầy giáo có bao nhiêu cách tặng cho các em học sinh sao cho sau khi tặng xong, mỗi một trong ba loại sách trên đều còn ít nhất một cuốn?
Quảng cáo
Trả lời:
Ta tìm số cách sao cho sau khi tặng sách xong có 1 môn hết sách.
TH1: Môn Toán hết sách:
Số cách chọn 4 cuốn sách Toán là 1 cách.
Số cách chọn 1 cuốn trong 6 cuốn còn lại là 6 cách.
Vậy có 6 cách chọn sách.
Số cách tặng 5 cuốn sách đó cho 5 em học sinh là cách.
Vậy có 6.120 = 720 cách.
TH2: Môn Lí hết sách:
Số cách chọn 3 cuốn sách Lí là 1 cách.
Số cách chọn 2 cuốn trong 7 cuốn còn lại là cách.
Vậy có 21 cách chọn sách.
Số cách tặng 5 cuốn sách đó cho 5 em học sinh là cách.
Vậy có 21.120 = 2 520 cách.
TH3: Môn Hóa hết sách: Tương tự trường hợp 2 thì có 2 520 cách.
Số cách chọn 5 cuốn bất kì trong 10 cuốn và tặng cho 5 em là cách.
Vậy số cách chọn sao cho sau khi tặng xong, mỗi loại sách trên đều còn lại ít nhất một cuốn là 30 240 – 720 – 2 520 – 2 520 = 24 480 cách.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: C

Số học sinh giỏi toán, lý mà không giỏi hóa: 3 – 1 = 2.
Số học sinh giỏi toán, hóa mà không giỏi lý: 4 – 1 = 3.
Số học sinh giỏi hóa, lý mà không giỏi toán: 2 – 1 = 1.
Số học sinh chỉ giỏi môn lý: 5 – 2 – 1 – 1 = 1.
Số học sinh chỉ giỏi môn hóa: 6 – 3 – 1 – 1 = 1.
Số học sinh chỉ giỏi môn toán: 7 – 3 – 2 – 1 = 1.
Số học sinh giỏi ít nhất một (môn toán, lý, hóa) là số học sinh giỏi 1 môn hoặc 2 môn hoặc cả 3 môn: 1 + 1 + 1 + 1 + 2 + 3 + 1 = 10.
Lời giải
Gọi x (triệu) đồng là số tiền mà doanh nghiệp A dự định giảm giá (0 ≤ x ≤ 4).
Khi đó:
Lợi nhuận thu được khi bán một chiếc xe là 31 – x – 27 = 4 – x (triệu đồng).
Số xe mà doanh nghiệp sẽ bán được trong một năm là 600 + 200x (chiếc).
Lợi nhuận mà doanh nghiệp thu được trong một năm là
f(x) = (4 − x)(600 + 200x) = −200x2 + 200x + 2400.
Xét hàm số f(x) = −200x2 + 200x + 2400 trên đoạn [0; 4] có bảng biến thiên:
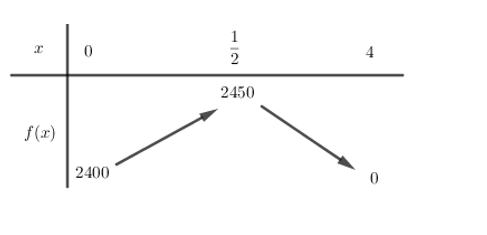
Vậy ⇔
Vậy giá mới của chiếc xe là 30,5 triệu đồng thì lợi nhuận thu được là cao nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số f(x) có bảng biến thiên như sau: Số nghiệm thuộc đoạn [π; 2π] của phương trình 2f(sin x) + 3 = 0 là: A. 4. B. 6. C. 3. D. 8. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid5-1694745831.png)