Câu hỏi:
19/09/2023 249
Cho hình thoi ABCD có AC = 8 và BD = 6. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
Cho hình thoi ABCD có AC = 8 và BD = 6. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
Đáp án chính xác
Câu hỏi trong đề:
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
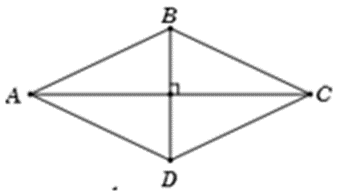
Gọi \(O = AC \cap BD\), giả thiết không cho góc, ta phân tích các vec tơ \(\overrightarrow {AB} ;\overrightarrow {AC} \) theo các vec tơ có giá vuông góc với nhau
Ta có:
\(\overrightarrow {AB} .\overrightarrow {AC} = (\overrightarrow {AO} + \overrightarrow {OB} ).\overrightarrow {AC} = \overrightarrow {AO} .\overrightarrow {AC} + \overrightarrow {OB} .\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AC} + 0 = \frac{1}{2}A{C^2} = 32\)
Vậy đáp án cần chọn là D.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian Oxyz, cho điểm A(2; 1; 3) và đường thẳng d: \(\frac{{x + 1}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z - 2}}{2}\). Đường thẳng đi qua A, vuông góc với d và cắt trục Oy có phương trình là:
Trong không gian Oxyz, cho điểm A(2; 1; 3) và đường thẳng d: \(\frac{{x + 1}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z - 2}}{2}\). Đường thẳng đi qua A, vuông góc với d và cắt trục Oy có phương trình là:
Xem đáp án »
19/09/2023
13,679
Câu 2:
Cho hàm số y = f(x) có bảng biến thiên như sau:
![Số nghiệm thuộc đoạn [0; 2pi] của phương trình f(cosx) = -2 là: A. 3 B. 0 C. 2 D. 1 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid18-1695111629.png)
Số nghiệm thuộc đoạn [0; 2π] của phương trình f(cosx) = –2 là:
Cho hàm số y = f(x) có bảng biến thiên như sau:
Số nghiệm thuộc đoạn [0; 2π] của phương trình f(cosx) = –2 là:
Xem đáp án »
19/09/2023
3,882
Câu 3:
Biết \(\int\limits_1^2 {\frac{{x + 1}}{{{x^2} + x\ln {\rm{x}}}}} d{\rm{x}} = \ln \left( {\ln a + b} \right)\) với a, b là các số nguyên dương. Tính P = a2 + ab + b2.
Biết \(\int\limits_1^2 {\frac{{x + 1}}{{{x^2} + x\ln {\rm{x}}}}} d{\rm{x}} = \ln \left( {\ln a + b} \right)\) với a, b là các số nguyên dương. Tính P = a2 + ab + b2.
Xem đáp án »
19/09/2023
3,694
Câu 4:
Cho hàm số f(x) có bảng biến thiên như sau:
![Số nghiệm thuộc đoạn [-pi; 2pi] của phương trình 2f(sinx) + 3 = 0 là: A. 4 B. 6 C. 3 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid12-1695110777.png)
Số nghiệm thuộc đoạn [–π; 2π] của phương trình 2f(sinx) + 3 = 0 là:
Cho hàm số f(x) có bảng biến thiên như sau:
Số nghiệm thuộc đoạn [–π; 2π] của phương trình 2f(sinx) + 3 = 0 là:
Xem đáp án »
19/09/2023
1,705
Câu 5:
Từ các số 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên chẵn gồm 5 chữ số đôi một khác nhau, đồng thời chia hết cho 9.
Từ các số 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên chẵn gồm 5 chữ số đôi một khác nhau, đồng thời chia hết cho 9.
Xem đáp án »
12/07/2024
1,683
Câu 6:
Cho hình nón đỉnh S, góc ở đỉnh bằng 120°, đáy là hình tròn (O; 3R). Cắt hình nón bởi mặt phẳng qua S và tạo với đáy góc 60°. Diện tích thiết diện là:
Cho hình nón đỉnh S, góc ở đỉnh bằng 120°, đáy là hình tròn (O; 3R). Cắt hình nón bởi mặt phẳng qua S và tạo với đáy góc 60°. Diện tích thiết diện là:
Xem đáp án »
19/09/2023
1,393
Câu 7:
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi E, F lần lượt là trung điểm của AB, BC. Đẳng thức nào sau đây sai?
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi E, F lần lượt là trung điểm của AB, BC. Đẳng thức nào sau đây sai?
Xem đáp án »
19/09/2023
1,222
về câu hỏi!