Câu hỏi:
13/07/2024 2,368
Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB, BC, CD, DA lần lượt tại các điểm M, N, P, Q.
a) Chứng minh rằng các đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.
Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB, BC, CD, DA lần lượt tại các điểm M, N, P, Q.
a) Chứng minh rằng các đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a)
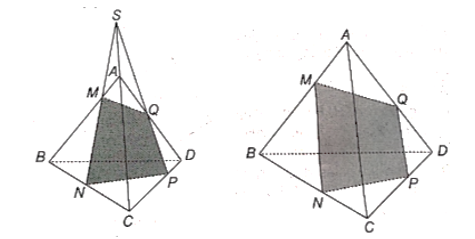
Ta có (ABC) ∩ (ACD) = AC;
(ABC) ∩ (MNPQ) = MN;
(ACD) ∩ (MNPQ) = PQ.
Khi đó ba mặt phẳng (ABC), (ACD) và (MNPQ) đôi một cắt nhau theo ba giao tuyến AC, MN, PQ. Áp dụng định lí về ba đường giao tuyến cho ba mặt phẳng trên, ta suy ra ba đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
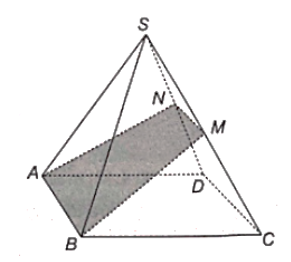
Giao tuyến của mặt phẳng (MAB) với mặt phẳng (ABCD) là AB.
Giao tuyến của mặt phẳng (MAB) với mặt phẳng (SAB) là AB.
Giao tuyến của mặt phẳng (MAB) với mặt phẳng (SBC) là MB.
Trong mặt phẳng (SCD), vẽ MN // CD (N ∈ SD).
Mà AB // CD (do ABCD là hình bình hành) nên MN // AB // CD.
Do đó, N thuộc mặt phẳng (MAB) nên giao tuyến của của mặt phẳng (MAB) với mặt phẳng (SCD) là MN và giao tuyến của mặt phẳng (MAB) với mặt phẳng (SAD) là NA.
Lời giải
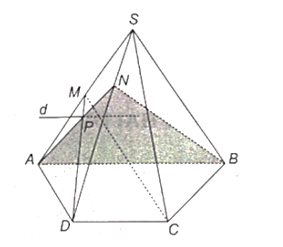
a) Trong mặt phẳng (SAD), gọi P là giao điểm của AN và DM.
Khi đó, hai mặt phẳng (NAB) và (MCD) có điểm chung P và lần lượt chứa hai đường thẳng AB và CD song song với nhau nên giao tuyến của hai mặt phẳng này là đường thẳng đi qua P là song song với AB, CD.
Trong mặt phẳng (NAB), vẽ đường thẳng d đi qua P và song song với AB thì d là giao tuyến cần tìm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
-
Bài tập Tổ hợp - Xác suất cơ bản, nâng cao có lời giải chi tiết (P6)
-
10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận