1. Lớp 11
  2. Toán
  3. Giải SGK Toán 11 KNTT Bài 11. Hai đường thẳng song song có đáp án

Giải SGK Toán 11 KNTT Bài 11. Hai đường thẳng song song có đáp án

362 lượt thi 21 câu hỏi

Đề thi liên quan:

Giải SGK Toán 11 KNTT Bài 10. Đường thẳng và mặt phẳng trong không gian có đáp án

415 lượt thi

Thi ngay

Giải SBT Toán 11 KNTT Bài 10. Đường thẳng và mặt phẳng trong không gian có đáp án

351 lượt thi

Thi ngay

Giải SBT Toán 11 KNTT Bài 11. Hai đường thẳng song song có đáp án

278 lượt thi

Thi ngay

Giải SGK Toán 11 KNTT Bài 12. Đường thẳng và mặt phẳng song song có đáp án

249 lượt thi

Thi ngay

Giải SBT Toán 11 KNTT Bài 12. Đường thẳng và mặt phẳng song song có đáp án

234 lượt thi

Thi ngay

Giải SGK Toán 11 KNTT Bài 13. Hai mặt phẳng song song có đáp án

337 lượt thi

Thi ngay

Giải SBT Toán 11 KNTT Bài 13. Hai mặt phẳng song song có đáp án

195 lượt thi

Thi ngay

Giải SGK Toán 11 KNTT Bài 14. Phép chiếu song song có đáp án

249 lượt thi

Thi ngay

Giải SBT Toán 11 KNTT Bài 14. Phép chiếu song song có đáp án

229 lượt thi

Thi ngay

Danh sách câu hỏi:

Câu 1:

Để giải quyết vấn đề tắc đường ở các thành phố lớn, có rất nhiều giải pháp được đưa ra. Trong đó giải pháp xây dựng các hệ thống cầu vượt, đường hoặc đường sắt trên cao đã và đang được đưa vào thực tế ở Việt Nam. Toán học mô tả vị trí tương quan giữa các tuyến đường trên như thế nào?
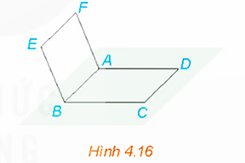
Media VietJack

Câu 2:

Hình 4.13 minh họa bốn tuyến đường (được coi là thẳng) tại một nút giao ở Hà Nội. Quan sát hình ảnh đó và trả lời các câu hỏi sau:

a) Hai tuyến đường nào giao nhau?

b) Hai tuyến đường nào không giao nhau?

c) Hai tuyến đường nào song song?

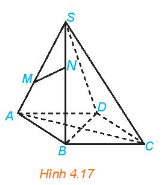
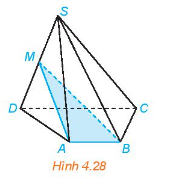
Media VietJack

Câu 3:

Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn.
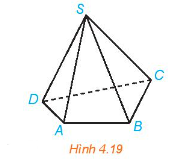
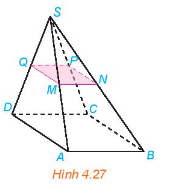
Media VietJack

Câu 4:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.17).

Media VietJack

a) Trong các đường thẳng AB, AC, CD, hai đường thẳng nào song song, hai đường thẳng nào cắt nhau?

b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh SA, SB. Trong các đường thẳng SA, MN, AB có hai đường thẳng nào chéo nhau hay không?

Câu 5:

Trong hình chóp tứ giác S.ABCD (H.4.19), chỉ ra những đường thẳng:

a) Chéo với đường thẳng SA;

b) Chéo với đường thẳng BC.

Media VietJack

Câu 6:

Một chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn (H.4.20). Hỏi có thể đặt chiếc gậy đó song song với một trong các mép tường hay không?
Media VietJack

Câu 7:

Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d.

Media VietJack

a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d?

b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?

Câu 8:

Quan sát lớp học và tìm hai đường thẳng song song với mép trên của bảng. Hai đường thẳng đó có song song với nhau hay không?

Câu 9:

Trong Ví dụ 1, chứng minh rằng bốn điểm C, D, E, F đồng phẳng và tứ giác CDFE là hình bình hành.
Media VietJack

Câu 10:

Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo các giao tuyến a và b khác c.

a) Nếu hai đường thẳng a và c cắt nhau tại M thì đường thẳng b có đi qua M hay không (H.4.23)? Giải thích vì sao.

Media VietJack

b) Nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c có song song với nhau hay không (H.4.24)? Giải thích vì sao.

Media VietJack

Câu 11:

Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).

Câu 12:

Một bể kính chứa nước có đáy là hình chữ nhật được đặt nghiêng như Hình 4.26. Giải thích tại sao đường mép nước AB song song với cạnh CD của bể nước.
Media VietJack

Câu 13:

Trong không gian, cho ba đường thẳng a, b, c. Những mệnh đề nào sau đây là đúng?

a) Nếu a và b không cắt nhau thì a và b song song.

b) Nếu b và c chéo nhau thì b và c không cùng thuộc một mặt phẳng.

c) Nếu a và b cùng song song với c thì a song song với b.

d) Nếu a và b cắt nhau, b và c cắt nhau thì a và c cắt nhau.

Câu 14:

Cho hình chóp S.ABCD có đáy là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau, cặp đường thẳng nào song song, cặp đường thẳng nào chéo nhau?

a) AB và CD;

b) AC và BD;

c) SB và CD.

Câu 15:

Cho hình chóp S.ABCD có đáy là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau, cặp đường thẳng nào song song, cặp đường thẳng nào chéo nhau?

a) AB và CD;

b) AC và BD;

c) SB và CD.

Câu 16:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành.
Media VietJack

Câu 17:

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng tứ giác MNCD là hình thang.

Câu 18:

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28).

a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD).

b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.

Media VietJack

Câu 19:

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28).

a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD).

b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.

Media VietJack

Câu 20:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC.

a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD).

b) Chứng minh rằng d song song với BD.

Câu 21:

(Đố vui) Khi hai cánh cửa sổ hình chữ nhật được mở, dù ở vị trí nào, thì hai mép ngoài của chúng luôn song song với nhau (H.4.29). Hãy giải thích tại sao.

Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30 thì có vị trí nào của hai cánh cửa để hai mép ngoài của chúng song song với nhau hay không?

Media VietJack
4.6

72 Đánh giá

50%

40%

0%

0%

0%

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.

Đăng ký

Bạn đã có tài khoản?