Giải SBT Toán 11 KNTT Bài 4. Phương trình lượng giác cơ bản có đáp án

Lời giải

a) \(2\sin \left( {\frac{x}{3} + 15^\circ } \right) + \sqrt 2 = 0\)

\( \Leftrightarrow \sin \left( {\frac{x}{3} + 15^\circ } \right) = - \frac{{\sqrt 2 }}{2}\)

\( \Leftrightarrow \sin \left( {\frac{x}{3} + 15^\circ } \right) = \sin \left( { - 45^\circ } \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}\frac{x}{3} + 15^\circ = - 45^\circ + k360^\circ \\\frac{x}{3} + 15^\circ = 180^\circ - \left( { - 45^\circ } \right) + k360^\circ \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}x = - 180^\circ + k1080^\circ \\x = 630^\circ + k1080^\circ \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).

b) \(\cos \left( {2x + \frac{\pi }{5}} \right) = - 1\)

\( \Leftrightarrow 2x + \frac{\pi }{5} = \pi + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow x = \frac{{2\pi }}{5} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

c) 3tan 2x + \(\sqrt 3 \) = 0

\( \Leftrightarrow \tan 2x =  - \frac{{\sqrt 3 }}{3}\)

\( \Leftrightarrow \tan 2x = \tan \left( { - \frac{\pi }{6}} \right)\)

\( \Leftrightarrow 2x = - \frac{\pi }{6} + k\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow x = - \frac{\pi }{{12}} + k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).

d) cot (2x – 3) = cot 15°

⇔ 2x – 3 = 15° + k180° (k ∈ ℤ)

⇔ 2x = 3 + 15° + k180° (k ∈ ℤ)

⇔ x = 1,5 + 7,5° + k90° (k ∈ ℤ).

Lời giải

a) Ta có sin(2x + 15°) + cos(2x – 15°) = 0

⇔ sin(2x + 15°) = – cos(2x – 15°)

⇔ sin(2x + 15°) = – sin[90° – (2x – 15°)]

⇔ sin(2x + 15°) = sin[– 90° + (2x – 15°)]

⇔ sin(2x + 15°) = sin(2x – 105°)

\( \Leftrightarrow \left[ \begin{array}{l}2x + 15^\circ = 2x - 105^\circ + k360^\circ \\2x + 15^\circ = 180^\circ - \left( {2x - 105^\circ } \right) + k360^\circ \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}120^\circ = k360^\circ \\x = 67,5^\circ + k90^\circ \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).

Không xảy ra trường hợp 120° = k360°.

Vậy phương trình đã cho có nghiệm x = 67,5° + k90° (k ∈ ℤ).

b) \(\cos \left( {2x + \frac{\pi }{5}} \right) + \cos \left( {3x - \frac{\pi }{6}} \right) = 0\)

\( \Leftrightarrow \cos \left( {2x + \frac{\pi }{5}} \right) = \cos \left[ {\pi - \left( {3x - \frac{\pi }{6}} \right)} \right]\)

\( \Leftrightarrow \cos \left( {2x + \frac{\pi }{5}} \right) = \cos \left( {\frac{{7\pi }}{6} - 3x} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}2x + \frac{\pi }{5} = \frac{{7\pi }}{6} - 3x + k2\pi \\2x + \frac{\pi }{5} = - \left( {\frac{{7\pi }}{6} - 3x} \right) + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{{29\pi }}{{150}} + k\frac{{2\pi }}{5}\\x = \frac{{41\pi }}{{30}} - k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).

c) Ta có tan x + cot x = 0

⇔ tan x = – cot x

⇔ tan x = cot(π – x)

\( \Leftrightarrow \tan x = \tan \left[ {\frac{\pi }{2} - \left( {\pi - x} \right)} \right]\)

\( \Leftrightarrow \tan x = \tan \left( {x - \frac{\pi }{2}} \right)\)

\( \Leftrightarrow x = x - \frac{\pi }{2} + k\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow \frac{\pi }{2} - k\pi = 0\,\,\left( {k \in \mathbb{Z}} \right)\). Vô lí.

Vậy phương trình đã cho vô nghiệm.

d) Điều kiện cos x ≠ 0 .

Ta có sin x + tan x = 0

\( \Leftrightarrow \sin x + \frac{{\sin x}}{{\cos x}} = 0\)

\( \Leftrightarrow \sin x\left( {1 + \frac{1}{{\cos x}}} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\1 + \frac{1}{{\cos x}} = 0\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\cos x = - 1\end{array} \right.\)

⇔ sin x = 0 (do sin² x + cos² x = 1)

⇔ x = kπ (k ∈ ℤ).

Vì x = kπ (k ∈ ℤ) thoả mãn điều kiện cos x ≠ 0 nên nghiệm của phương trình đã cho là

x = kπ (k ∈ ℤ).

Lời giải

a) Ta có (2 + cos x)(3cos 2x – 1) = 0

\( \Leftrightarrow \left[ \begin{array}{l}2 + \cos x = 0\\3\cos 2x - 1 = 0\end{array} \right.\)

+ Phương trình 2 + cos x = 0 vô nghiệm vì – 1 ≤ cos x ≤ 1.

+ Gọi α là góc thoả mãn cos α = \(\frac{1}{3}\). Ta có

3cos 2x – 1 = 0 ⇔ cos 2x = cos α ⇔ 2x = ± α + k2π (k ∈ ℤ) ⇔ x = \( \pm \frac{\alpha }{2}\) + kπ (k ∈ ℤ).

Vậy nghiệm của phương trình đã cho là x = \( \pm \frac{\alpha }{2}\) + kπ (k ∈ ℤ) với cos α = \(\frac{1}{3}\).

b) Ta có 2sin 2x – sin 4x = 0

⇔ 2sin 2x – 2sin 2x cos 2x = 0

⇔ 2sin 2x(1 – cos2x) = 0

\( \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\\cos 2x = 1\end{array} \right.\)

Do sin² 2x + cos² 2x = 1 nên cos 2x = 1 kéo theo sin 2x = 0, do đó phương trình đã cho tương đương với

sin 2x = 0 ⇔ 2x = kπ (k ∈ ℤ) \( \Leftrightarrow x = k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).

c) Ta có cos⁶ x – sin⁶ x = 0

⇔ cos⁶ x = sin⁶ x

⇔ (cos² x)³ = (sin² x)³

⇔ cos² x = sin² x

⇔ cos² x – sin² x = 0

⇔ cos 2x = 0

Từ đó ta được 2x = \(\frac{\pi }{2}\) + kπ (k ∈ ℤ) hay \(x = \frac{\pi }{4} + k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).

d) Điều kiện sin x ≠ 0 và cos 2x ≠ 0.

Ta có tan 2x cot x = 1

\( \Leftrightarrow \tan 2x = \frac{1}{{\cot x}}\)

⇔ tan 2x = tan x

⇔ 2x = x + kπ   (k ∈ ℤ)

⇔ x = kπ   (k ∈ ℤ).

Ta thấy x = kπ (k ∈ ℤ) không thoả mãn điều kiện sin x ≠ 0.

Vậy phương trình đã cho vô nghiệm.

Lời giải

a) Giá trị tương ứng của hai hàm số \(y = \cos \left( {2x - \frac{\pi }{3}} \right)\) và \(y = \cos \left( {x - \frac{\pi }{4}} \right)\) bằng nhau nếu

\(\cos \left( {2x - \frac{\pi }{3}} \right) = \cos \left( {x - \frac{\pi }{4}} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}2x - \frac{\pi }{3} = x - \frac{\pi }{4} + k2\pi \\2x - \frac{\pi }{3} = - \left( {x - \frac{\pi }{4}} \right) + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{12}} + k2\pi \\x = \frac{{7\pi }}{{36}} + k\frac{{2\pi }}{3}\,\end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

b) Giá trị tương ứng của hai hàm số \(y = \sin \left( {3x - \frac{\pi }{4}} \right)\) và \(y = \sin \left( {x - \frac{\pi }{6}} \right)\) bằng nhau nếu

\(\sin \left( {3x - \frac{\pi }{4}} \right) = \sin \left( {x - \frac{\pi }{6}} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}3x - \frac{\pi }{4} = x - \frac{\pi }{6} + k2\pi \\3x - \frac{\pi }{4} = \pi - \left( {x - \frac{\pi }{6}} \right) + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)

Lời giải

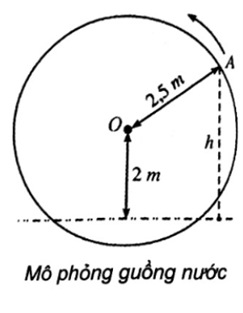
a) Vì \( - 1 \le \sin 2\pi \left( {x - \frac{1}{4}} \right) \le 1\) nên \( - 2,5 \le 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) \le 2,5\) và do đó ta có

\(2 - 2,5 \le 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) \le 2 + 2,5\)

hay \( - 0,5 \le 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) \le 4,5\,\,\forall x \in \mathbb{R}\).

Suy ra, gầu ở vị trí cao nhất khi \(\sin 2\pi \left( {x - \frac{1}{4}} \right) = 1\)\( \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow x = \frac{1}{2} + k\,\,\left( {k \in \mathbb{Z}} \right)\). Do x ≥ 0 nên \(x = \frac{1}{2} + k\,\,\left( {k \in \mathbb{N}} \right)\).

Vậy gầu ở vị trí cao nhất tại các thời điểm \(\frac{1}{2},\,\,\frac{3}{2},\,\,\frac{5}{2},...\) phút.

Tương tự, gầu ở vị trí thấp nhất khi \(\sin 2\pi \left( {x - \frac{1}{4}} \right) = - 1\)\( \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = - \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow x = k\,\,\left( {k \in \mathbb{Z}} \right)\). Do x ≥ 0 nên \(x = k\,\,\left( {k \in \mathbb{N}} \right)\).

Vậy gàu ở vị trí thấp nhất tại các thời điểm 0, 1, 2, 3, ... phút.

b) Gầu cách mặt nước 2 m khi \(2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) = 2\)

\( \Leftrightarrow \sin 2\pi \left( {x - \frac{1}{4}} \right) = 0\)

\( \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = k\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow x = \frac{1}{4} + \frac{k}{2}\,\,\left( {k \in \mathbb{Z}} \right)\).

Do x ≥ 0 nên \(x = \frac{1}{4} + \frac{k}{2}\,\,\left( {k \in \mathbb{N}} \right)\).

Vậy chiếc gầu cách mặt nước 2 m lần đầu tiên tại thời điểm \(x = \frac{1}{4}\) phút.

Lời giải

Vì \( - 1 \le \sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right) \le 1\) nên \( - 2,83 \le 2,83\sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right) \le 2,83\), do đó

\(12 - 2,83 \le 12 + 2,83\sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right) \le 12 + 2,83\)

hay \(9,17 \le 12 + 2,83\sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right) \le 14,83\,\,\,\forall t \in \mathbb{R}\).

a) Ngày thành phố A có ít giờ ánh sáng mặt trời nhất ứng với \(\sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right) = - 1\)

\( \Leftrightarrow \frac{{2\pi }}{{365}}\left( {t - 80} \right) = - \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow t = - \frac{{45}}{4} + 365k\,\,\left( {k \in \mathbb{Z}} \right)\)

Vì 0 < t ≤ 365 nên k = 1 suy ra t = \( - \frac{{45}}{4}\) + 365 = 353,75.

Như vậy, vào ngày thứ 353 của năm, tức là khoảng ngày 20 tháng 12 thì thành phố A sẽ có ít giờ ánh sáng mặt trời nhất.

b) Ngày thành phố A có nhiều giờ ánh sáng mặt trời nhất ứng với \(\sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right) = 1\)

\( \Leftrightarrow \frac{{2\pi }}{{365}}\left( {t - 80} \right) = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow t = \frac{{685}}{4} + 365k\,\,\left( {k \in \mathbb{Z}} \right)\)

Vì 0 < t ≤ 365 nên k = 0 suy ra t = \(\frac{{685}}{4}\) = 171,25.

Như vậy, vào ngày thứ 171 của năm, tức là khoảng ngày 20 tháng 6 thì thành phố A sẽ có nhiều giờ ánh sáng mặt trời nhất.

c) Thành phố A có khoảng 10 giờ ánh sáng mặt trời trong ngày nếu

\(12 + 2,83\sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right) = 10\)

\[ \Leftrightarrow \sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right) = - \frac{{200}}{{283}}\]

\( \Leftrightarrow \left[ \begin{array}{l}\frac{{2\pi }}{{365}}\left( {t - 80} \right) \approx - 0,78 + k2\pi \\\frac{{2\pi }}{{365}}\left( {t - 80} \right) \approx 3,93 + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)

Từ đó ta được \(\left[ \begin{array}{l}t \approx 34,69 + 365k\\t \approx 308,3 + 365k\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).

Vì 0 < t ≤ 365 nên k = 0 suy ra t ≈ 34,69 hoặc t ≈ 308,3.

Như vậy, vào khoảng ngày thứ 34 của năm, tức là ngày 3 tháng 2 và ngày thứ 308 của năm, tức là ngày 4 tháng 11 thành phố A sẽ có 10 giờ ánh sáng mặt trời.