Giải SBT Toán 11 KNTT Bài 26. Khoảng cách có đáp án

53 người thi tuần này 4.6 893 lượt thi 9 câu hỏi

Đề số 1

🔥 Học sinh cũng đã học

35 người thi tuần này

Đề thi giữa kì 1 Toán 11 năm 2026-2027 THPT Việt Đức (Hà Nội) có đáp án

134 lượt thi 21 câu hỏi

24 người thi tuần này

Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Tạ Quang Bửu (Hà Nội) có đáp án

123 lượt thi 21 câu hỏi

40 người thi tuần này

Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Nguyễn Bỉnh Khiêm (Hà Nội) có đáp án

139 lượt thi 22 câu hỏi

69 người thi tuần này

Trắc nghiệm Công thức nhân xác suất cho hai biến cố độc lập lớp 11 (có đúng sai, trả lời ngắn)

1.6 K lượt thi 20 câu hỏi

60 người thi tuần này

Trắc nghiệm Công thức cộng xác suất lớp 11 (có đúng sai, trả lời ngắn)

2.4 K lượt thi 20 câu hỏi

216 người thi tuần này

Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Phùng Khắc Khoan (Thạch Thất-Hà Nội) có đáp án - mã đề 2345

3 K lượt thi 21 câu hỏi

97 người thi tuần này

Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Phùng Khắc Khoan (Thạch Thất-Hà Nội) có đáp án - mã đề 0123

2.9 K lượt thi 21 câu hỏi

76 người thi tuần này

Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Vạn Xuân (Hoài Đức-Hà Nội) có đáp án - Đề chẵn

2.8 K lượt thi 21 câu hỏi

Danh sách câu hỏi:

Câu 1/9

Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh bằng a, SA $⊥$ (ABC) và SA = 2a. Tính theo a khoảng cách:

a) Từ điểm B đến mặt phẳng (SAC).

Xem đáp án

Lời giải

Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh bằng a (ảnh 1)

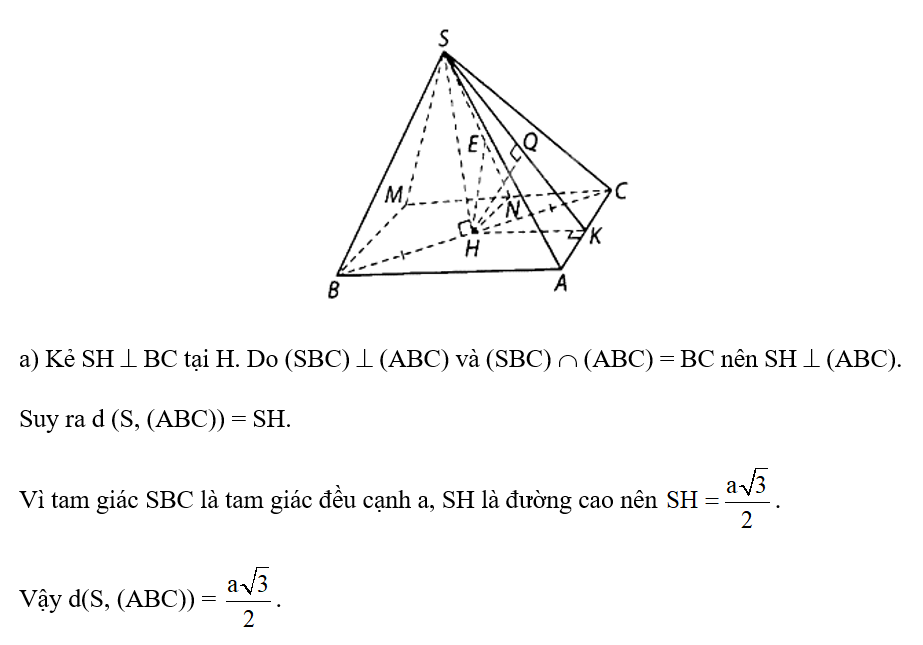
a) Kẻ BH $⊥$ AC tại H.

Vì SA $⊥$ (ABC) nên SA $⊥$ BH mà BH $⊥$ AC. Suy ra, BH $⊥$ (SAC).

Vì ABC là tam giác đều cạnh a có BH là đường cao nên $B H = \frac{a \sqrt{3}}{2}$ .

Do đó d(B, (SAC)) = BH = $\frac{a \sqrt{3}}{2}$ .

Câu 2/9

b) Từ điểm A đến mặt phẳng (SBC).

Xem đáp án

Lời giải

b) Kẻ AM $⊥$ BC tại M, AK $⊥$ SM tại K

Do SA $⊥$ (ABC) nên SA $⊥$ BC mà AM $⊥$ BC nên BC $⊥$ (SAM), suy ra BC $⊥$ AK.

Vì AK $⊥$ SM và BC $⊥$ AK thì AK $⊥$ (SBC).

Suy ra d(A, (SBC)) = AK.

Tam giác ABC đều cạnh bằng a có AM là đường cao nên $A M = \frac{a \sqrt{3}}{2}$ .

Vì SA $⊥$ (ABC) nên SA $⊥$ AM.

Xét tam giác SAM vuông tại A, có $\frac{1}{A K^{2}} = \frac{1}{S A^{2}} + \frac{1}{A M^{2}} = \frac{1}{4 a^{2}} + \frac{4}{3 a^{2}} = \frac{19}{12 a^{2}}$ . Vậy d(A, (SBC)) = $\Rightarrow A K = 2 a \sqrt{\frac{3}{19}}$ .

Câu 3/9

c) Giữa hai đường thẳng AB và SC.

Xem đáp án

Lời giải

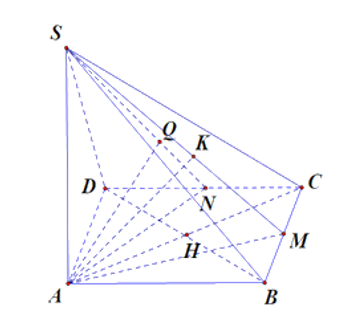
c) Dựng hình bình hành ABCD thì AB // CD nên AB // (SCD) và mặt phẳng (SCD) chứa SC nên d(AB, SC) = d(AB, (SCD)). Mà d(AB, (SCD)) = d(A, (SCD)).

Kẻ AN $⊥$ DC tại N, kẻ AQ $⊥$ SN tại Q

Vì ADC là tam giác đều, AN là đường cao nên $A N = \frac{a \sqrt{3}}{2}$ .

Vì SA $⊥$ (ABC) nên SA $⊥$ (ABCD), suy ra SA $⊥$ DC mà AN $⊥$ DC nên DC $⊥$ (SAN).

Vì DC $⊥$ (SAN) nên DC $⊥$ AQ mà AQ $⊥$ SN nên AQ $⊥$ (SDC).

Khi đó d(A, (SCD)) = AQ.

Xét tam giác SAN vuông tại A, có $\frac{1}{A Q^{2}} = \frac{1}{S A^{2}} + \frac{1}{A N^{2}} = \frac{1}{4 a^{2}} + \frac{4}{3 a^{2}} = \frac{19}{12 a^{2}}$ , $\Rightarrow A Q = 2 a \sqrt{\frac{3}{19}}$ . Vậy d(AB, SC) = $2 a \sqrt{\frac{3}{19}}$ .

Câu 4/9

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, góc ABC bằng 60°, biết tam giác SBC đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính theo a khoảng cách:

a) Từ điểm S đến mặt phẳng (ABC).

Xem đáp án

Lời giải

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, góc ABC bằng (ảnh 1)

Câu 5/9

b) Từ điểm B đến mặt phẳng (SAC).

Xem đáp án

Lời giải

b) Từ điểm B đến mặt phẳng (SAC). (ảnh 1)

Câu 6/9

c) Giữa hai đường thẳng AB và SC.

Xem đáp án

Lời giải

c) Giữa hai đường thẳng AB và SC. (ảnh 1)

c) Giữa hai đường thẳng AB và SC. (ảnh 2)

Câu 7/9

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A và AB = AC = AA' = a. Tính theo a khoảng cách:

a) Từ điểm A đến đường thẳng B'C'.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8/9

b) Giữa hai đường thẳng BC và AB'.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9/9

Trên một mái nhà nghiêng 30° so với mặt phẳng nằm ngang, người ta dựng một chiếc cột vuông góc với mái nhà. Hỏi chiếc cột tạo với mặt phẳng nằm ngang một góc bao nhiêu độ? Vì sao?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 3/9 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh bằng a, SA $⊥$ (ABC) và SA = 2a. Tính theo a khoảng cách:

a) Từ điểm B đến mặt phẳng (SAC).