Giải SBT Toán 11 KNTT Bài 23. Đường thẳng vuông góc với mặt phẳng có đáp án

39 người thi tuần này 4.6 0.9 K lượt thi 9 câu hỏi

Đề số 1

🔥 Học sinh cũng đã học

49 người thi tuần này

Bài tập Vận dụng đạo hàm cấp hai để giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)

1.1 K lượt thi 10 câu hỏi

42 người thi tuần này

Bài tập Vận dụng các quy tắc tính đạo hàm để giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)

1.1 K lượt thi 10 câu hỏi

30 người thi tuần này

Bài tập Sử dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương các hàm số và đạo hàm của hàm số hợp lớp 11 (có lời giải)

1 K lượt thi 10 câu hỏi

34 người thi tuần này

Bài tập Vận dụng định nghĩa đạo hàm vào giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)

1.3 K lượt thi 10 câu hỏi

48 người thi tuần này

Bài tập Thiết lập phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị lớp 11 (có lời giải)

1.3 K lượt thi 10 câu hỏi

32 người thi tuần này

Bài tập Các bài toán thực tiễn vận dụng công thức nhân xác suất lớp 11 (có lời giải)

1.4 K lượt thi 10 câu hỏi

34 người thi tuần này

Bài tập Tính xác suất của biến cố hợp của hai biến cố bất kì bằng cách sử dụng công thức cộng xác suất và phương pháp tổ hợp lớp 11 (có lời giải)

1.4 K lượt thi 10 câu hỏi

30 người thi tuần này

Bài tập Biến cố độc lập lớp 11 (có lời giải)

4.2 K lượt thi 10 câu hỏi

Danh sách câu hỏi:

Câu 1/9

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy là tam giác ABC vuông tại B. Kẻ AM vuông góc với SB tại M và AN vuông góc với SC tại N. Chứng minh rằng:

a) BC $⊥$ (SAB);

b) AM $⊥$ (SBC);

c) SC $⊥$ (AMN).

Xem đáp án

Lời giải

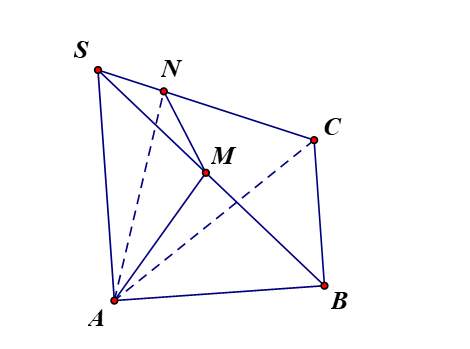
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy là tam giác ABC vuông (ảnh 1)

a) Vì SA

⊥

(ABC) nên SA

⊥

BC mà AB

⊥

BC (do tam giác ABC vuông tại B). Do đó BC

⊥

(SAB).

b) Vì BC $⊥$ (SAB) nên BC $⊥$ AM, mà AM $⊥$ SB (giả thiết). Do đó AM $⊥$ (SBC).

c) Vì AM $⊥$ (SBC) nên AM $⊥$ SC, mà AN $⊥$ SC (giả thiết). Do đó SC ^ (AMN).

Câu 2/9

Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi H là chân đường vuông góc hạ từ O đến mặt phẳng (ABC). Chứng minh rằng:

a) BC $⊥$ (OAH);

Xem đáp án

Lời giải

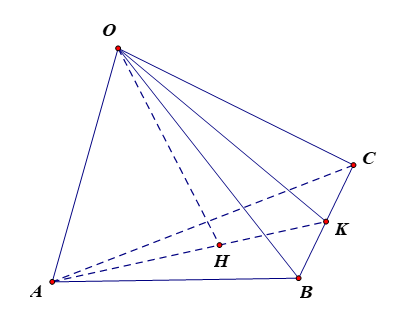
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi (ảnh 1)

a) Vì OA $⊥$ OB, OA $⊥$ OC nên OA $⊥$ (OBC). Suy ra OA $⊥$ BC.

Mà OH $⊥$ (ABC) nên OH $⊥$ BC. Do đó BC $⊥$ (OAH).

Câu 3/9

b) H là trực tâm của tam giác ABC;

Xem đáp án

Lời giải

b) Vì BC $⊥$ (OAH) nên BC $⊥$ AH, do đó AH là đường cao của tam giác ABC. (1)

Có OH $⊥$ (ABC) nên OH $⊥$ AC.

Có OB $⊥$ OA, OC $⊥$ OB nên OB $⊥$ (OAC) nên OB $⊥$ AC mà OH $⊥$ AC, từ đó suy ra AC $⊥$ (OBH), suy ra CA ^ BH, do đó BH là đường cao của tam giác ABC. (2)

Từ (1) và (2) suy ra H là giao hai đường cao của tam giác ABC.

Do đó H là trực tâm của tam giác ABC.

Câu 4/9

c) $\frac{1}{O H^{2}} = \frac{1}{O A^{2}} + \frac{1}{O B^{2}} + \frac{1}{O C^{2}}$ .

Xem đáp án

Lời giải

c) Gọi K là giao điểm của AH với BC.

Vì OA ^ (OBC) nên OA ^ OK .

Xét tam giác OAK vuông tại O, có OH là đường cao nên $\frac{1}{O H^{2}} = \frac{1}{O A^{2}} + \frac{1}{O K^{2}}$ .

Vì AK ^ BC mà OA ^ BC nên BC ^ (OAK), suy ra OK ^ BC.

Xét tam giác OBC vuông tại O, có OK là đường cao nên $\frac{1}{O K^{2}} = \frac{1}{O B^{2}} + \frac{1}{O C^{2}}$ .

Do đó $\frac{1}{O H^{2}} = \frac{1}{O A^{2}} + \frac{1}{O B^{2}} + \frac{1}{O C^{2}}$ .

Câu 5/9

Cho tứ diện ABCD có AB = AC và DB = DC. Chứng minh rằng AD $⊥$ BC.

Xem đáp án

Lời giải

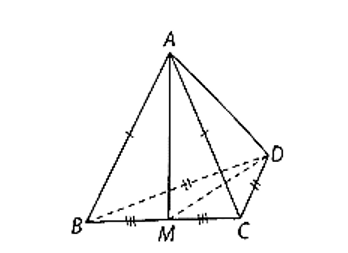
Cho tứ diện ABCD có AB = AC và DB = DC. Chứng minh rằng AD vuông góc BC. (ảnh 1)

Gọi M là trung điểm của BC.

Xét tam giác ABC có AB = AC và AM là trung tuyến nên AM là đường cao.

Do đó AM $⊥$ BC. (1)

Xét tam giác BCD có DC = DB và DM là trung tuyến nên DM là đường cao.

Do đó DM $⊥$ BC. (2)

Từ (1) và (2) có: BC $⊥$ (ADM). Suy ra BC $⊥$ AD.

Câu 6/9

Cho hình lăng trụ tam giác ABC.A'B'C' có AA' vuông góc với mặt phẳng (ABC) và đáy là tam giác ABC vuông tại B. Chứng minh rằng:

a) BB' $⊥$ (A'B'C');

b) B'C' $⊥$ (ABB'A').

Xem đáp án

Lời giải

Cho hình lăng trụ tam giác ABC.A'B'C' có AA' vuông góc với mặt phẳng (ABC) và đáy là tam giác (ảnh 1)

Câu 7/9

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Chứng minh rằng:

a) SO $⊥$ (ABCD);

b) AC $⊥$ (SBD) và BD $⊥$ (SAC).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8/9

Cho hình chóp S.ABC có SA ^ (ABC), tam giác ABC nhọn. Gọi H, K lần lượt là trực tâm của tam giác ABC và SBC. Chứng minh rằng:

a) BC $⊥$ (SAH) và các đường thẳng AH, BC, SK đồng quy;

b) SB $⊥$ (CHK) và HK $⊥$ (SBC).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9/9

Một cây cột được dựng trên một sàn phẳng. Người ta thả dây dọi và ngắm thấy cột song song với dây dọi. Hỏi có thể khẳng định rằng cây cột vuông góc với sàn hay không? Vì sao?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 3/9 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Toán

Toán

Toán

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Toán

Toán

Toán

Tiếng Việt

Tiếng Anh

Giải SBT Toán 11 KNTT Bài 23. Đường thẳng vuông góc với mặt phẳng có đáp án

🔥 Học sinh cũng đã học

Bài tập Vận dụng đạo hàm cấp hai để giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)

Bài tập Vận dụng các quy tắc tính đạo hàm để giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)

Bài tập Sử dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương các hàm số và đạo hàm của hàm số hợp lớp 11 (có lời giải)

Bài tập Vận dụng định nghĩa đạo hàm vào giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)

Bài tập Thiết lập phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị lớp 11 (có lời giải)

Bài tập Các bài toán thực tiễn vận dụng công thức nhân xác suất lớp 11 (có lời giải)

Bài tập Tính xác suất của biến cố hợp của hai biến cố bất kì bằng cách sử dụng công thức cộng xác suất và phương pháp tổ hợp lớp 11 (có lời giải)

Bài tập Biến cố độc lập lớp 11 (có lời giải)

Danh sách câu hỏi:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy là tam giác ABC vuông tại B. Kẻ AM vuông góc với SB tại M và AN vuông góc với SC tại N. Chứng minh rằng: a) BC ⊥ (SAB); b) AM ⊥(SBC); c) SC ⊥ (AMN).

Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi H là chân đường vuông góc hạ từ O đến mặt phẳng (ABC). Chứng minh rằng: a) BC ⊥ (OAH);

b) H là trực tâm của tam giác ABC;

c) 1OH2=1OA2+1OB2+1OC2.

Cho tứ diện ABCD có AB = AC và DB = DC. Chứng minh rằng AD ⊥ BC.

Cho hình lăng trụ tam giác ABC.A'B'C' có AA' vuông góc với mặt phẳng (ABC) và đáy là tam giác ABC vuông tại B. Chứng minh rằng: a) BB' ⊥ (A'B'C'); b) B'C' ⊥ (ABB'A').

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Chứng minh rằng: a) SO ⊥(ABCD); b) AC ⊥ (SBD) và BD ⊥ (SAC).

Cho hình chóp S.ABC có SA ^ (ABC), tam giác ABC nhọn. Gọi H, K lần lượt là trực tâm của tam giác ABC và SBC. Chứng minh rằng: a) BC ⊥ (SAH) và các đường thẳng AH, BC, SK đồng quy; b) SB ⊥ (CHK) và HK ⊥ (SBC).

Một cây cột được dựng trên một sàn phẳng. Người ta thả dây dọi và ngắm thấy cột song song với dây dọi. Hỏi có thể khẳng định rằng cây cột vuông góc với sàn hay không? Vì sao?

Xem tiếp với tài khoản VIP

Đăng ký

Đăng nhập

Quên mật khẩu

CHỌN BỘ SÁCH BẠN MUỐN XEM

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy là tam giác ABC vuông tại B. Kẻ AM vuông góc với SB tại M và AN vuông góc với SC tại N. Chứng minh rằng:

a) BC $⊥$ (SAB);

b) AM $⊥$ (SBC);

c) SC $⊥$ (AMN).

Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi H là chân đường vuông góc hạ từ O đến mặt phẳng (ABC). Chứng minh rằng:

a) BC $⊥$ (OAH);

c) $\frac{1}{O H^{2}} = \frac{1}{O A^{2}} + \frac{1}{O B^{2}} + \frac{1}{O C^{2}}$ .

Cho tứ diện ABCD có AB = AC và DB = DC. Chứng minh rằng AD $⊥$ BC.

Cho hình lăng trụ tam giác ABC.A'B'C' có AA' vuông góc với mặt phẳng (ABC) và đáy là tam giác ABC vuông tại B. Chứng minh rằng:

a) BB' $⊥$ (A'B'C');

b) B'C' $⊥$ (ABB'A').

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Chứng minh rằng:

a) SO $⊥$ (ABCD);

b) AC $⊥$ (SBD) và BD $⊥$ (SAC).

Cho hình chóp S.ABC có SA ^ (ABC), tam giác ABC nhọn. Gọi H, K lần lượt là trực tâm của tam giác ABC và SBC. Chứng minh rằng:

a) BC $⊥$ (SAH) và các đường thẳng AH, BC, SK đồng quy;

b) SB $⊥$ (CHK) và HK $⊥$ (SBC).