Chuyên đề Toán 11 KNTT Bài tập cuối chuyên đề 1 có đáp án
40 người thi tuần này 4.6 667 lượt thi 8 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Danh sách câu hỏi:
Lời giải
Lời giải:
a) Ta có: 2 . (– 1) – 2 – 1 = – 5 ≠ 0 nên A(– 1; 2) không thuộc ∆.
Gọi H là chân đường vuông góc hạ từ A xuống ∆.
Vì H thuộc ∆ nên H(x; 2x – 1). Ta có: \(\overrightarrow {AH} = \left( {x + 1;\,2x - 3} \right)\), vectơ chỉ phương của đường thẳng ∆ là \(\overrightarrow {{u_\Delta }} = \left( {1;\,2} \right)\).
Vì AH vuông góc với ∆ nên \(\overrightarrow {AH} .\overrightarrow {{u_\Delta }} = 0 \Leftrightarrow \left( {x + 1} \right).1 + \left( {2x - 3} \right).2 = 0\).
Từ đó suy ra x = 1 nên H(1; 1).
Vì A' là ảnh của điểm A qua phép đối xứng trục ∆ nên AA' vuông góc với ∆ tại H và H là trung điểm của AA'. Suy ra \[\left\{ \begin{array}{l}{x_{A'}} = 2{x_H} - {x_A} = 2.1 - \left( { - 1} \right) = 3\\{y_{A'}} = 2{y_H} - {y_A} = 2.1 - 2 = 0\end{array} \right.\]. Vậy A'(3; 0).
b)
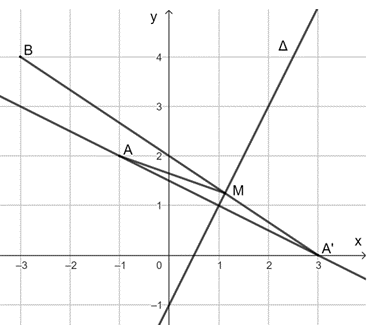
Ta có: 2 . (– 3) – 4 – 1 = – 11; 2 . (– 1) – 2 – 1 = – 5 và (– 11) . (– 5) = 55 > 0 nên hai điểm A và B nằm về một phía của đường thẳng ∆.
Vì M thuộc ∆ và A và A' đối xứng nhau qua ∆ nên MA = MA' và A' và B nằm về hai phía của đường thẳng ∆.
Do đó, MA + MB = MA' + MB đạt giá trị nhỏ nhất khi M là giao điểm của A'B và ∆.
Ta có: \(\overrightarrow {A'B} = \left( { - 6;\,4} \right)\), suy ra \(\overrightarrow {{n_{A'B}}} = \left( {2;\,3} \right)\) là một vectơ pháp tuyến của đường thẳng A'B. Phương trình đường thẳng A'B là 2(x – 3) + 3(y – 0) = 0 hay 2x + 3y – 6 = 0.
Tọa độ giao điểm M của A'B và ∆ là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x - y - 1 = 0\\2x + 3y - 6 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{9}{8}\\y = \frac{5}{4}\end{array} \right.\). Vậy \(M\left( {\frac{9}{8};\,\frac{5}{4}} \right)\).
Lời giải
Lời giải:
Cách 1:
Lấy A(0; 5), B(1; 7) thuộc đường thẳng d.
Gọi A', B' tương ứng là ảnh của A, B qua phép tịnh tiến theo vectơ \(\overrightarrow u \left( { - 3;\,4} \right)\).
Khi đó: \(\overrightarrow {AA'} = \overrightarrow u \,\,\)và \(\overrightarrow {BB'} = \overrightarrow u \). Suy ra A'(– 3; 9) và B'(– 2; 11).
Vì đường thẳng d' là ảnh của đường thẳng d qua phép tịnh tiến theo vectơ \(\overrightarrow u \left( { - 3;\,4} \right)\) nên hai điểm A', B' thuộc đường thẳng d'.
Ta có: \(\overrightarrow {A'B'} = \left( {1;\,2} \right)\), suy ra đường thẳng d' có một vectơ pháp tuyến là \(\overrightarrow n = \left( {2;\, - 1} \right)\).
Phương trình đường thẳng d' là 2(x + 3) – (y – 9) = 0 hay 2x – y + 15 = 0.
Cách 2:
Gọi M(x; y) thuộc đường thẳng d và M'(x'; y') là ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow u \left( { - 3;\,4} \right)\). Khi đó \(\overrightarrow {MM'} = \overrightarrow u \)\( \Leftrightarrow \left\{ \begin{array}{l}x' - x = - 3\\y' - y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 3\\y = y' - 4\end{array} \right.\).
Ta có M thuộc ∆ ⇔ 2x – y + 5 = 0 ⇔ 2(x' + 3) – (y' – 4) + 5 = 0 ⇔ 2x' – y' + 15 = 0. Do đó, M'(x'; y') thuộc đường thẳng có phương trình 2x – y + 15 = 0.
Vì đường thẳng d' là ảnh của đường thẳng d qua phép tịnh tiến theo vectơ \(\overrightarrow u \left( { - 3;\,4} \right)\) nên M' thuộc đường thẳng d'.
Vậy phương trình đường thẳng d' là 2x – y + 15 = 0.
Lời giải
Lời giải:
Ta có (C): x2 + y2 – 2x – 4y – 4 = 0 hay x2 + y2 – 2 . 1 x – 2 . 2 y – 4 = 0.
Suy ra đường tròn (C) có tâm I(1; 2) và bán kính R = \(\sqrt {{1^2} + {2^2} - \left( { - 4} \right)} = 3\).
Gọi I' và R' lần lượt là tâm và bán kính của đường tròn (C'). Vì (C') là ảnh của (C) qua phép đối xứng tâm A(3; – 3) nên I' là ảnh của I qua phép đối xứng tâm A(3; – 3) và R' = R = 3.
Vì I' là ảnh của I qua phép đối xứng tâm A nên A là trung điểm của II'.
Suy ra \(\left\{ \begin{array}{l}{x_{I'}} = 2{x_A} - {x_I} = 2.3 - 1 = 5\\{y_{I'}} = 2{y_A} - {y_I} = 2.\left( { - 3} \right) - 2 = - 8\end{array} \right.\) nên I'(5; – 8).
Vậy phương trình đường tròn (C') là
(x – 5)2 + [y – (– 8)]2 = 32 hay (x – 5)2 + (y + 8)2 = 9.
Lời giải
Lời giải:
Ta có (C): (x – 1)2 + (y + 2)2 = 9 hay (x – 1)2 + [y – (– 2)]2 = 32.
Suy ra đường tròn (C) có tâm I(1; – 2) và bán kính R = 3.
Gọi I' và R' lần lượt là tâm và bán kính của đường tròn (C'). Vì (C') là ảnh của (C) qua phép vị tự tâm O(0; 0) với tỉ số k = – 2 nên I' là ảnh của I qua phép vị tự tâm O(0; 0) với tỉ số k = – 2 và R' = |– 2|.R = 2 . 3 = 6.
Vì I' là ảnh của I qua phép vị tự V(O, – 2) nên \(\overrightarrow {OI'} = - 2\overrightarrow {OI} \).
Suy ra \[\left\{ \begin{array}{l}{x_{I'}} = - 2{x_I} = - 2.1 = - 2\\{y_{I'}} = - 2{y_I} = - 2.\left( { - 2} \right) = 4\end{array} \right.\] nên I'(– 2; 4).
Vậy phương trình đường tròn (C') là
[x – (– 2)]2 + (y – 4)2 = 62 hay (x + 2)2 + (y – 4)2 = 36.
Lời giải
Lời giải:
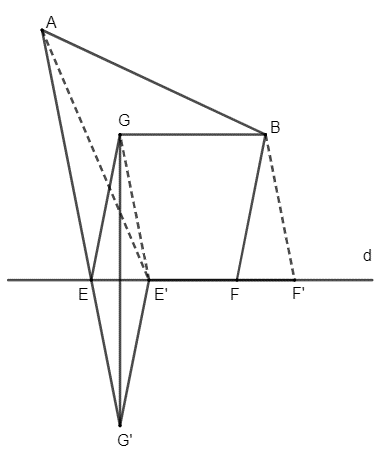
Ta có: \(\left| {\overrightarrow {EF} } \right| = m\) (m > 0) không đổi.
Đặt \(\overrightarrow u = \overrightarrow {EF} \) \(\left( {\overrightarrow u \ne \overrightarrow 0 } \right)\), \(\overrightarrow u \) không đổi, khi đó \(\left| {\overrightarrow u } \right| = m\) không đổi.
Gọi G là ảnh của điểm B qua phép tịnh tiến theo vectơ \( - \overrightarrow u \). Khi đó \(\overrightarrow {BG} = - \overrightarrow u \). Vì B cố định và \(\overrightarrow u \) không đổi nên G cố định. Gọi G' là ảnh của G qua phép đối xứng trục d thì G' cố định.
Gọi giao điểm của AG' và đường thẳng d là E, trên d lấy điểm F thỏa mãn EF = m và \(\overrightarrow {EF} = \overrightarrow u = - \overrightarrow {BG} \) hay \(\overrightarrow {EF} = \overrightarrow {GB} \). Khi đó BGEF là hình bình hành nên BF = GE.
Mà G và G' đối xứng nhau qua d nên GE = G'E. Do đó BF = GE = G'E.
Ta có: AE + BF = AE + G'E = AG' (1).
Ta có E và F như trên là hai điểm cần tìm để AE + BF nhỏ nhất.
Thật vậy, gọi E' và F' là 2 điểm trên d, khác E và F sao cho \(\overrightarrow {E'F'} = \overrightarrow u \) và \(\left| {\overrightarrow {E'F'} } \right| = \left| {\overrightarrow u } \right| = m\).
Ta có: AE' + BF' = AE' + GE' = AE' + G'E' > AG' (2) (bất đẳng thức trong tam giác AG'E').
Từ (1) và (2) suy ra AE + BF < AE' + BF'. Từ đó suy ra điều phải chứng minh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
