Giải SBT Toán 11 KNTT Bài 10. Đường thẳng và mặt phẳng trong không gian có đáp án
33 người thi tuần này 4.6 0.9 K lượt thi 21 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
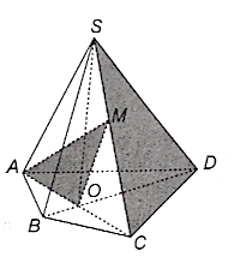
a) Ta có AO cắt CD tại C nên C ∈ AO ⊂ (AMO) và C ∈ CD ⊂ (SCD).
Do đó, C ∈ (AMO) ∩ (SCD).
Lại có M ∈ SC ⊂ (SCD) và M ∈ (AMO) nên M ∈ (AMO) ∩ (SCD).
Vậy giao tuyến của hai mặt phẳng (AMO) và (SCD) là đường thẳng MC hay chính là đường thẳng SC.
Lời giải
b) Ta có BO cắt CD tại D nên D ∈ BO ⊂ (BMO) và D ∈ CD ⊂ (SCD).
Do đó, D ∈ (BMO) ∩ (SCD).
Lại có M ∈ SC ⊂ (SCD) và M ∈ (BMO) nên M ∈ (BMO) ∩ (SCD).
Vậy giao tuyến của hai mặt phẳng (BMO) và (SCD) là đường thẳng DM.
Lời giải
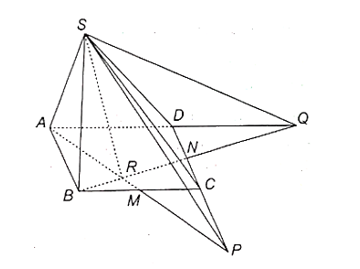
a) Trong mặt phẳng (ABCD), gọi P là giao điểm của AM và CD.
Khi đó P ∈ (SAM) ∩ (SCD).
Mà S ∈ (SAM) ∩ (SCD).
Vậy SP là giao tuyến của hai mặt phẳng (SAM) và (SCD).
Lời giải
b) Trong mặt phẳng (ABCD), gọi Q là giao điểm của BN và AD.
Khi đó Q ∈ (SBN) ∩ (SAD).
Mà S ∈ (SBN) ∩ (SAD).
Vậy SQ là giao tuyến của hai mặt phẳng (SBN) và (SAD).
Lời giải
c) Trong mặt phẳng (ABCD), gọi R là giao điểm của AM và BN.
Khi đó R ∈ (SAM) ∩ (SBN).
Mà S ∈ (SAM) ∩ (SBN).
Vậy SR là giao tuyến của hai mặt phẳng (SAM) và (SBN).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.