Giải SBT Toán 11 KNTT Bài 1. Giá trị lượng giác của góc lượng giác có đáp án
25 người thi tuần này 4.6 1.2 K lượt thi 9 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 7 (có lời giải) - Đề 1
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 3
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 2
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 1
Đề kiểm tra Bài tập cuối chương 6 (có lời giải) - Đề 3
Danh sách câu hỏi:
Lời giải
Ta có: \(20^\circ = 20.\frac{\pi }{{180}} = \frac{\pi }{9}\); \(150^\circ = 150.\frac{\pi }{{180}} = \frac{{5\pi }}{6}\); \(500^\circ = 500.\frac{\pi }{{180}} = \frac{{25\pi }}{9}\);
\(\frac{{11\pi }}{2} = \frac{{11\pi }}{2}.\left( {\frac{{180}}{\pi }} \right)\begin{array}{*{20}{c}}^\circ \\{}\end{array} = 990^\circ \); \(\frac{{ - 5\pi }}{6} = \frac{{ - 5\pi }}{6}.\left( {\frac{{180}}{\pi }} \right)\begin{array}{*{20}{c}}^\circ \\{}\end{array} = - 150^\circ \); \(\frac{{7\pi }}{{15}} = \frac{{7\pi }}{{15}}.\left( {\frac{{180^\circ }}{\pi }} \right) = 84^\circ \).
Khi đó ta có
|
Số đo độ |
20° |
990° |
150° |
500° |
– 150° |
84° |
|
Số đo rađian |
\(\frac{\pi }{9}\) |
\(\frac{{11\pi }}{2}\) |
\(\frac{{5\pi }}{6}\) |
\(\frac{{25\pi }}{9}\) |
\(\frac{{ - 5\pi }}{6}\) |
\(\frac{{7\pi }}{{15}}\) |
Lời giải
a) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là \(\frac{\pi }{6}\) được xác định như hình dưới đây.
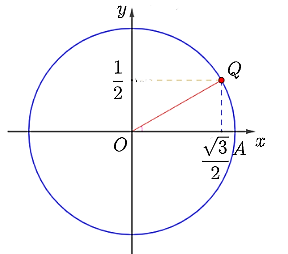
b) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là \(\frac{{ - 5\pi }}{7}\) được xác định như hình dưới đây.
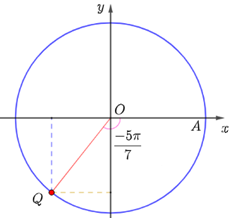
c) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là 270° được xác định như hình dưới đây.
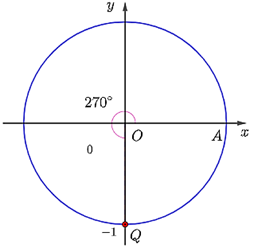
d) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là – 415° được xác định như hình dưới đây.
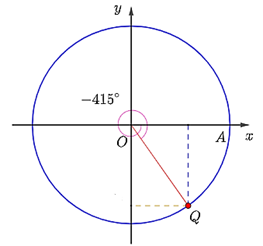
Lời giải
Lời giải
a) Ta có l = Rα = 20 . \(\frac{{2\pi }}{7} = \frac{{40\pi }}{7}\) (m).
b) Ta có l = R . \(\frac{{\pi a}}{{180}} = 20.\frac{{\pi .36}}{{180}} = 4\pi \) (m).
Lời giải
Lời giải
Từ đẳng thức sin2 x + cos2 x = 1, suy ra
sin2 x = 1 – cos2 x = \(1 - {\left( { - \frac{5}{{13}}} \right)^2} = \frac{{144}}{{169}}\)
Mặt khác 90° < x < 180° nên sinx > 0. Do đó sin x = \(\sqrt {\frac{{144}}{{169}}} = \frac{{12}}{{13}}\).
Suy ra tan x = \(\frac{{\sin x}}{{\cos x}} = \frac{{12}}{{13}}:\left( { - \frac{5}{{13}}} \right) = - \frac{{12}}{5}\), cot x = \(\frac{{\cos x}}{{\sin x}} = \left( { - \frac{5}{{13}}} \right):\frac{{12}}{{13}} = - \frac{5}{{12}}\).
Lời giải
Lời giải
a) Ta có: sin a + cos a = m nên (sin a + cos a)2 = m2
hay sin2 a + cos2 a + 2sin a cos a = m2 hay 1 + 2sin a cos a = m2.
Từ đó suy ra sin a cos a = \(\frac{{{m^2} - 1}}{2}\).
b) sin3 a + cos3 a = (sin a + cos a)3 – 3sin a cos a(sin a + cos a)
= m3 – 3m\(\frac{{{m^2} - 1}}{2} = \frac{{3m - {m^3}}}{2}\).
c) sin4 a + cos4 a = (sin2 a + cos2 a)2 – 2sin2 a cos2 a
= 1 – 2(sin a cos a)2 = \(1 - 2.{\left( {\frac{{{m^2} - 1}}{2}} \right)^2} = 1 - \frac{{{{\left( {{m^2} - 1} \right)}^2}}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.