Giải SBT Toán 11 KNTT Bài 24. Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng có đáp án
27 người thi tuần này 4.6 729 lượt thi 8 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 8
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 7
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 6
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 5
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 2
Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 1
Danh sách câu hỏi:
Lời giải
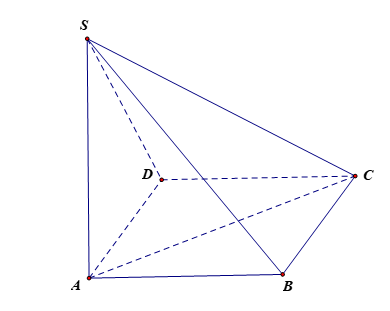
Kẻ AH ^ (BCD) tại H, ta có BH là hình chiếu vuông góc của AB trên mặt phẳng (BCD) nên góc giữa đường thẳng AB và mặt phẳng (BCD) bằng góc giữa hai đường AB và BH, mà (AB, BH) = .
Vì AB = AC = AD nên HD = HB = HC hay H là tâm của tam giác BCD.
Gọi M là giao điểm của BH là CD.
Vì tam giác BCD đều cạnh a nên BM là đường cao, trung tuyến và , suy ra .
Xét tam giác ABH vuông tại H có: .
Vậy côsin của góc giữa đường thẳng AB và mặt phẳng (BCD) bằng .
Lời giải
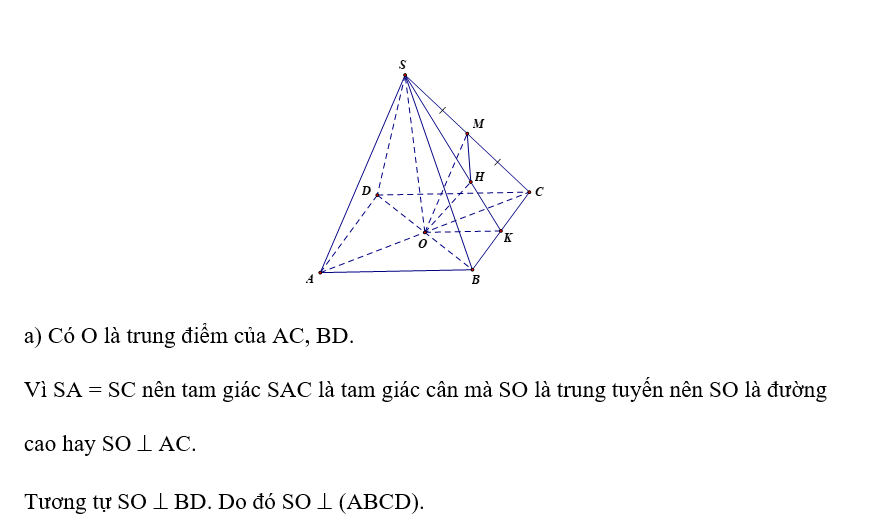
a) Vì SA ^ (ABCD) nên AC là hình chiếu vuông góc của SC trên mặt phẳng (ABCD). Do đó góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng SC và AC, mà (SC, AC) = .
Do ABCD là hình vuông cạnh a nên AC2 = AB2 + BC2 = 2a2 ⇒.
Vì SA ^ (ABCD) nên SA ^ AC mà nên tam giác SAC vuông cân tại A. Do đó .
Vậy góc giữa đường thẳng SC và mặt phẳng (ABCD) là 45°.
Lời giải
b) Vì SA ^ (ABCD) nên BC ^ SA mà BC ^ AB nên BC ^ (SAB), suy ra SB là hình chiếu vuông góc của SC trên mặt phẳng (SAB).
Do đó, góc giữa đường thẳng SC và mặt phẳng (SAB) bằng góc giữa đường thẳng SC và đường thẳng SB, mà .
Xét tam giác SAB vuông tại A, có
Xét tam giác SBC vuông tại B, ta có: .
Vậy tang của góc giữa đường thẳng SC và mặt phẳng (SAB) bằng .
Lời giải
Gọi O là giao điểm của A'C' và B'D'.
Khi đó, O là trung điểm của A'C' và B'D'.
Theo đề bài ta có O là hình chiếu của A trên mặt phẳng (A'B'C'D').
Do đó, A'O là hình chiếu vuông góc của AA' trên mặt phẳng (A'B'C'D'). Khi đó góc giữa đường thẳng AA' và mặt phẳng (A'B'C'D') bằng góc giữa AA' và A'O. Mà .
Vì hình hộp ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a nên A'B'C'D' là hình vuông cạnh a. Do đó A'C'2 = A'B'2 + B'C'2 = a2 + a2 = 2a2 ⇒ .
.
Vậy góc giữa đường thẳng AA' và mặt phẳng (A'B'C'D') bằng 60°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.