Câu hỏi:

11/07/2024 612

Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người. Kết quả như sau:

- Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B.

- Một người mỗi ngày cần từ 400 đến 1000 đơn vị vitamin cả A và B.

Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn \[\frac{1}{2}\] số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A. Biết giá một đơn vị vitamin A là 9 đồng và giá một đơn vị vitamin B là 7,5 đồng. Tìm phương án dùng hai loại vitamin A, B thoả mãn các điều kiện trên để có số tiền phải trả là ít nhất.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi x là số đơn vị vitamin A mỗi người tiếp nhận trong một ngày (x ≥ 0)

Gọi y là số đơn vị vitamin A mỗi người tiếp nhận trong một ngày (y ≥ 0)

Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B nên x ≤ 600 và y ≤ 500.

Một người mỗi ngày cần từ 400 đến 1000 đơn vị vitamin cả A và B nên:

400 ≤ x + y ≤ 1000

Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A nên: \[\left\{ \begin{array}{l}y \ge \frac{1}{2}x\\y \le 3x\end{array} \right.\]

Ta có hệ bất phương trình giữa x và y:

\[\left\{ \begin{array}{l}x \le 600\\y \le 500\\x + y \ge 400\\x + y \le 1000\\y \ge \frac{1}{2}x\\y \le 3x\end{array} \right.\]

Biểu diễn miền nghiệm của hệ bất phương trình:

- Biểu diễn miền nghiệm D₁ của bất phương trình x ≤ 600:

+ Vẽ đường thẳng d₁: x = 600 trên mặt phẳng tọa độ Oxy.

+ Thay x = 0, y = 0 vào bất phương trình ta được 0 ≤ 600 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x ≤ 600.

Vậy miền nghiệm D₁ của bất phương trình x ≤ 600 là nửa mặt phẳng bờ d₁ (kể cả bờ d₁) chứa điểm O.

* Tương tự ta biểu diễn các miền nghiệm:

- Miền nghiệm D₂ của bất phương trình y ≤ 500: là nửa mặt phẳng bờ d₂ (kể cả bờ d₂: y = 500) chứa điểm O.

- Miền nghiệm D₃ của bất phương trình x + y ≥ 400: là nửa mặt phẳng bờ d₃ (kể cả bờ d₃: x + y = 400) không chứa điểm O.

- Miền nghiệm D₄ của bất phương trình x + y ≤ 1000: là nửa mặt phẳng bờ d₄ (kể cả bờ d₄: x + y = 1000) chứa điểm O.

- Miền nghiệm D₅ của bất phương trình \[y \ge \frac{1}{2}x\]: là nửa mặt phẳng bờ d₅ (kể cả bờ d₅: \[y = \frac{1}{2}x\]) chứa điểm M(0; 50).

- Miền nghiệm D₆ của bất phương trình y ≤ 3x: là nửa mặt phẳng bờ d₆ (kể cả bờ d₆: y = 3x) không chứa điểm M (0; 50).

Ta có đồ thị sau:

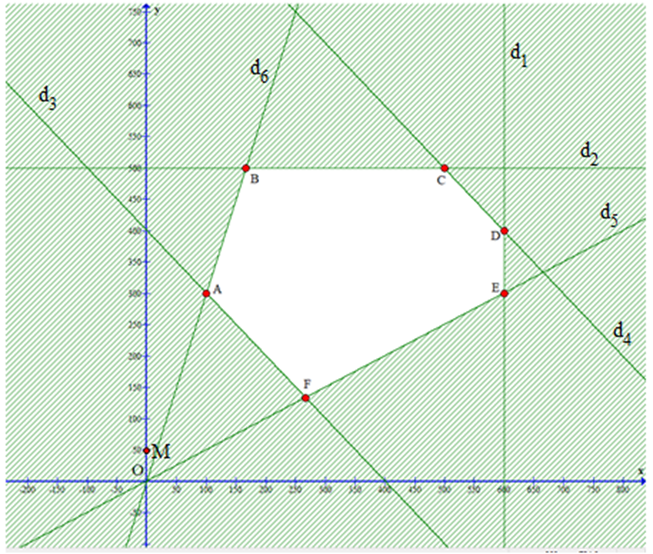
Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với (ảnh 1)

Miền nghiệm của hệ bất phương trình là miền của đa giác ABCDEF với:

A(100; 300); \[B\left( {\frac{{500}}{3};500} \right)\]; C(500; 500); D(600; 400); E(600; 300); \[F\left( {\frac{{800}}{3};\frac{{400}}{3}} \right)\]

Số tiền trả cho x đơn vị vitamin A và y đơn vị vitamin B là: F (x; y) = 9x + 7,5y.

Để có số tiền phải trả là ít nhất thì F(x; y) phải nhỏ nhất.

• Tại A(100; 300): F = 9.100 + 7,5. 300 = 3150;

• Tại \[B\left( {\frac{{500}}{3};500} \right)\]: F = 9. + 7,5. 500 = 5250;

• Tại C(500; 500): F = 9. 500 + 7,5. 500 = 8250;

• Tại D(600, 400): F = 9. 600 + 7,5. 400 = 8400;

• Tại E(600, 300): F = 9. 600 + 7,5. 300 = 7650;

• Tại \[F\left( {\frac{{800}}{3};\frac{{400}}{3}} \right)\], ta có: \[9 \cdot \frac{{800}}{3} + 7,5 \cdot \frac{{400}}{3} = 3\,\,400\]

Vậy F(x; y) nhỏ nhất là 3150 khi x =100 và y = 300.

Vậy mỗi người sẽ dùng 100 đơn vị vitamin A và 300 đơn vị vitamin B để đảm bảo các điều kiện số lượng sử dụng và chi phí phải trả là ít nhất.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số y = ax³+ bx²+ cx + d (a, b, c, d ∈ ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?

Xem đáp án

Lời giải

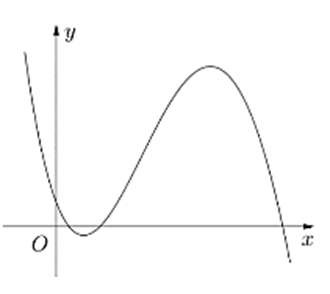
Từ đồ thị ta có: \[\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\]

Gọi x₁ và x₂ lần lượt là hai điểm cực trị của hàm số đã cho (x₁< x₂)

Từ đồ thị ta thấy: x₁ + x₂ > 0

Þ ab < 0 Þ b > 0

Lại có: x₁.x₂ > 0 Þ ac > 0 Þ c > 0

Đồ thị hàm số giao với trục tung tại điểm có tung độ y

Þ d > 0

Vậy trong các số a, b, c, d có 2 số dương.

Câu 2

Cho A = (m; m + 1); B = (1; 4). Tìm m để \[A \cap B \ne \emptyset \].

Xem đáp án

Lời giải

Để \[A \cap B \ne \emptyset \] thì \[\left\{ \begin{array}{l}m + 1 \le 1\\m \ge 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge 4\end{array} \right.\]

Vậy để \[A \cap B \ne \emptyset \] thì m Î (0; 4).

Câu 3