Cho p, q là số nguyên tố và phương trình x2 − px + q = 0 có nghiệm nguyên dương. Tìm p, q.

Câu hỏi:

11/07/2024 625

Cho p, q là số nguyên tố và phương trình x² − px + q = 0 có nghiệm nguyên dương. Tìm p, q.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Để phương trình đã cho có nghiệm nguyên dương thì Δ = p² − 4q là số chính phương.

Đặt p²− 4q = k² ⇔ 4q = (p − k)(p + k) với k là số tự nhiên.

Do p − k, p + k cùng tính chẵn, lẻ mà tích của chúng chẵn nên hai số này cùng chẵn.

Mặt khác p − k < p + k và q là số nguyên tố nên:

p − k = 2 và p + k = 2q hoặc p − k = 4 và p + k = q

Nếu p − k = 4 và p + k = q thì q chẵn do đó q = 2 (vô lí vì p + k > p − k).

Nếu p − k = 2 và p + k = 2q thì 2p = 2q + 2 tức p = q + 1. Do đó q chẵn tức q = 2. Suy ra p = 3.

Thử lại ta thấy phương trình: x² − 3x + 2= 0 có nghiệm nguyên dương x = 1 và x = 2.

Vậy p = 3; q = 2.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số y = ax³+ bx²+ cx + d (a, b, c, d ∈ ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?

Xem đáp án

Lời giải

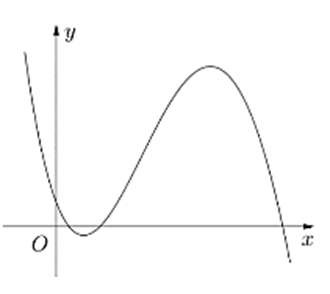
Từ đồ thị ta có: \[\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\]

Gọi x₁ và x₂ lần lượt là hai điểm cực trị của hàm số đã cho (x₁< x₂)

Từ đồ thị ta thấy: x₁ + x₂ > 0

Þ ab < 0 Þ b > 0

Lại có: x₁.x₂ > 0 Þ ac > 0 Þ c > 0

Đồ thị hàm số giao với trục tung tại điểm có tung độ y

Þ d > 0

Vậy trong các số a, b, c, d có 2 số dương.

Câu 2

Cho A = (m; m + 1); B = (1; 4). Tìm m để \[A \cap B \ne \emptyset \].

Xem đáp án

Lời giải

Để \[A \cap B \ne \emptyset \] thì \[\left\{ \begin{array}{l}m + 1 \le 1\\m \ge 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge 4\end{array} \right.\]

Vậy để \[A \cap B \ne \emptyset \] thì m Î (0; 4).

Câu 3