Giải phương trình: \(\frac{{\sqrt {1 - \sin 2{\rm{x}}} + \sqrt {1 + \sin 2{\rm{x}}} }}{{{\mathop{\rm s}\nolimits} {\rm{inx}}}} = 4c{\rm{osx}}\).
Giải phương trình: \(\frac{{\sqrt {1 - \sin 2{\rm{x}}} + \sqrt {1 + \sin 2{\rm{x}}} }}{{{\mathop{\rm s}\nolimits} {\rm{inx}}}} = 4c{\rm{osx}}\).
Quảng cáo
Trả lời:
Điều kiện: sinx ≠ 0
Ta có: \(\frac{{\sqrt {1 - \sin 2{\rm{x}}} + \sqrt {1 + \sin 2{\rm{x}}} }}{{{\mathop{\rm s}\nolimits} {\rm{inx}}}} = 4c{\rm{osx}}\)
\( \Rightarrow \sqrt {1 - \sin 2{\rm{x}}} + \sqrt {1 + \sin 2{\rm{x}}} = 4c{\rm{osxsinx}}\)
\[ \Rightarrow {\left( {\sqrt {1 - \sin 2{\rm{x}}} + \sqrt {1 + \sin 2{\rm{x}}} } \right)^2} = {\left( {2.2c{\rm{osxsinx}}} \right)^2}\] với sinxcosx > 0
\[ \Leftrightarrow 1 - \sin 2{\rm{x}} + 1 + \sin 2{\rm{x + 2}}\sqrt {\left( {1 - \sin 2{\rm{x}}} \right)\left( {1 + \sin 2{\rm{x}}} \right)} = {\left( {2{\rm{sin2x}}} \right)^2}\] với sin2x > 0
\[ \Leftrightarrow 2{\rm{ + 2}}\sqrt {1 - {{\sin }^2}2x} = 4{\rm{si}}{{\rm{n}}^2}{\rm{2x}}\] với sin2x > 0
\[ \Leftrightarrow 1{\rm{ + }}\sqrt {{{\cos }^2}2x} = 2{\rm{si}}{{\rm{n}}^2}{\rm{2x}}\] với sin2x > 0
⇔ 1 + |cos2x| = 2 – cos22x, với sin2x > 0
⇔ 2|cos2x|2 + |cos2x| – 1 = 0, với sin2x > 0
Đặt |cos2x| = t (t ≥ 0), ta có phương trình:
2t2 + t – 1 = 0 ⇔ (2t – 1)(t + 1) = 0\( \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{2}\,\,\left( {tm} \right)\\t = - 1\,\,\left( {ktm} \right)\end{array} \right.\)
Suy ra \(\left| {cos2{\rm{x}}} \right| = \frac{1}{2}\) nên \(co{s^2}2{\rm{x}} = \frac{1}{4} \Rightarrow {\sin ^2}2x = \frac{3}{4}\)
Mà sin2x > 0 nên \(\sin 2x = \frac{{\sqrt 3 }}{2}\)
Suy ra \(\left[ \begin{array}{l}2{\rm{x}} = \frac{\pi }{3} + k2\pi \\2{\rm{x}} = \pi - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = \frac{\pi }{6} + k\pi \\{\rm{x}} = \frac{\pi }{3} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vậy \({\rm{x}} = \frac{\pi }{6} + k\pi ;{\rm{x}} = \frac{\pi }{3} + k\pi \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 500 đơn vị vitamin A và 500 đơn vị vitamin B.
B. 600 đơn vị vitamin A và 400 đơn vị vitamin B.
C. 600 đơn vị vitamin A và 300 đơn vị vitamin B.
D. 100 đơn vị vitamin A và 300 đơn vị vitamin B.
Lời giải
Đáp án đúng là: D
Gọi x là số đơn vị vitamin A mỗi người tiếp nhận trong một ngày (x ≥ 0).
Gọi y là số đơn vị vitamin A mỗi người tiếp nhận trong một ngày (y ≥ 0).
Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B nên x ≤ 600 và y ≤ 500.
Một người mỗi ngày cần từ 400 đến 1 000 đơn vị vitamin cả A và B nên:
400 ≤ x + y ≤ 1000
Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn \(\frac{1}{2}\) số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A nên:
\(\left\{ \begin{array}{l}y \ge \frac{1}{2}x\\y \le 3{\rm{x}}\end{array} \right.\)
Ta có hệ bất phương trình giữa x và y: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x \le 600\\y \le 500\\x + y \ge 400\\x + y \le 1000\\y \ge \frac{1}{2}x\\y \le 3{\rm{x}}\end{array} \right.\)
Biểu diễn miền nghiệm của hệ bất phương trình:
− Biểu diễn miền nghiệm D1 của bất phương trình x ≤ 600
+ Vẽ đường thẳng d1: x = 600 trên mặt phẳng tọa độ Oxy
+ Thay x = 0, y = 0 vào bất phương trình ta được 0 ≤ 600 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x ≤ 600
Vậy miền nghiệm D1 của bất phương trình x ≤ 600 là nửa mặt phẳng bờ d1 (kể cả bờ d1) chứa điểm O.
Tương tự ta biểu diễn các miền nghiệm:
− Miền nghiệm D2 của bất phương trình y ≤ 500: là nửa mặt phẳng bờ d2 (kể cả bờ d2: y = 500) chứa điểm O.
− Miền nghiệm D3 của bất phương trình x + y ≥ 400: là nửa mặt phẳng bờ d3 (kể cả bờ d3: x + y = 400) không chứa điểm O.
− Miền nghiệm D4 của bất phương trình x + y ≤ 1000: là nửa mặt phẳng bờ d4 (kể cả bờ d4: x + y = 1000) chứa điểm O.
− Miền nghiệm D5 của bất phương trình \(y \ge \frac{1}{2}x\): là nửa mặt phẳng bờ d5 (kể cả bờ d5: \(y = \frac{1}{2}x\) ) chứa điểm M(0; 50).
− Miền nghiệm D6 của bất phương trình y ≤ 3x: là nửa mặt phẳng bờ d6 (kể cả bờ d6: y = 3x) không chứa điểm M (0; 50).
Ta có đồ thị sau:
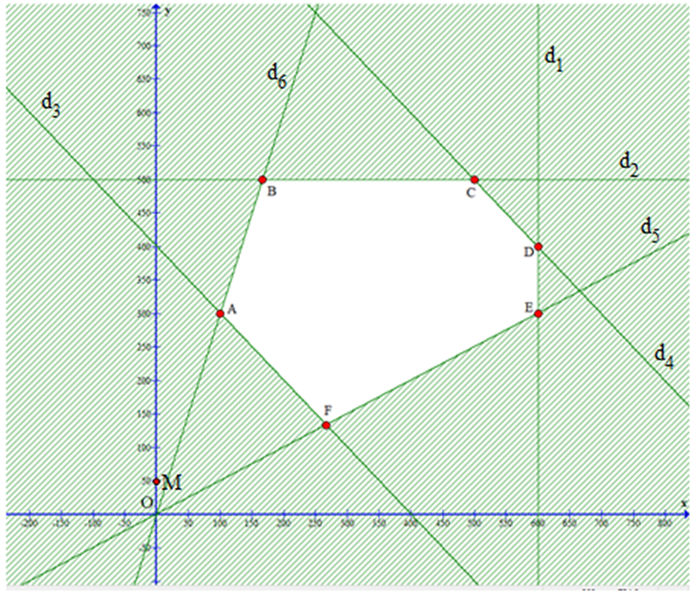
Miền nghiệm của hệ bất phương trình là miền của đa giác ABCDEF với: \(A\left( {100;300} \right),B\left( {\frac{{500}}{3};500} \right),C\left( {500;500} \right),D\left( {600;400} \right),E\left( {600;300} \right);F\left( {\frac{{800}}{3};\frac{{400}}{3}} \right)\)
Số tiền trả cho x đơn vị vitamin A và y đơn vị vitamin B là: F(x; y) = 9x + 7,5y
Để có số tiền phải trả là ít nhất thì F(x; y) phải nhỏ nhất
Tại A(100; 300): F = 9.100 + 7,5. 300 = 3150;
Tại \(B\left( {\frac{{500}}{3};500} \right):F = 9.\frac{{500}}{3} + 7,5.500 = 5250\)
Tại C(500; 500): F = 9. 500 + 7,5. 500 = 8250;
Tại D(600, 400): F = 9. 600 + 7,5. 400 = 8400;
Tại E(600, 300): F = 9. 600 + 7,5. 300 = 7650;
Tại \(F\left( {\frac{{800}}{3};\frac{{400}}{3}} \right):F = 9.\frac{{800}}{3} + 7,5.\frac{{400}}{3} = 3400\).
Suy ra F(x; y) nhỏ nhất là 3150 khi x = 100 và y = 300
Do đó mỗi người sẽ dùng 100 đơn vị vitamin A và 300 đơn vị vitamin B để đảm bảo các điều kiện số lượng sử dụng và chi phí phải trả là ít nhất
Vậy ta chọn đáp án D.
Câu 2
A. \(\frac{{4\pi }}{3}\)
B. \(\frac{{5\pi }}{3}\)
C. \(\frac{{7\pi }}{3}\)
D. \(\frac{{8\pi }}{3}\).
Lời giải
Đáp án đúng là: D
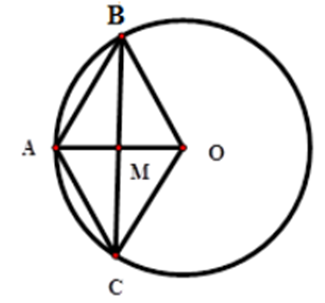
Vì độ dài đường tròn là 4π nên 4π = 2π . R
Suy ra R = 2 (cm)
Xét tứ giác ABOC có hai đường chéo AO và BC vuông góc với nhau tại trung điểm M nên ABOC là hình thoi
Suy ra OB = OC = AB
Do đó tam giác ABO đều nên \(\widehat {AOB} = 60^\circ \)
Suy ra \(\widehat {BOC} = 2\widehat {AOB} = 2.60^\circ = 120^\circ \)
Do đó số đo cung lớn BC là 360° – 120° = 240°
Độ dài cung lớn BC là \(l = \frac{{\pi .2.240^\circ }}{{180^\circ }} = \frac{{8\pi }}{3}\) (cm)
Vậy ta chọn đáp án D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
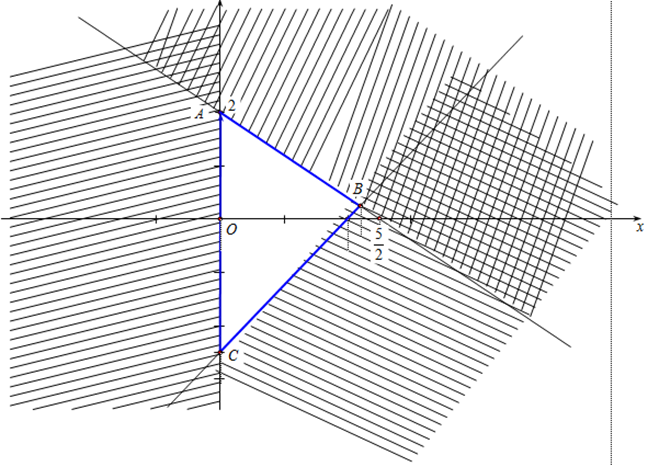
A. \(\left\{ \begin{array}{l}y \ge 0\\5{\rm{x}} - 4y \ge 10\\5{\rm{x}} + 4y \le 10\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x \ge 0\\{\rm{4x}} - 5y \le 10\\5{\rm{x}} + 4y \le 10\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x \ge 0\\5{\rm{x}} - 4y \le 10\\{\rm{4x}} + 5y \le 10\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x > 0\\5{\rm{x}} - 4y \le 10\\{\rm{4x}} + 5y \le 10\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.