Câu hỏi:

11/07/2024 155

Một hình nón có thiết diện qua trục là một tam giác đều cạnh a.

a) Tính diện tích xung quanh và diện tihcs toàn phần của hình nón

b) Tính thể tích của khối nón

c) Tính diệc tích của thiết diện

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa... kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 70k).

Tổng ôn Toán-lý hóa Văn-sử-đia Tiếng anh & các môn khác

Quảng cáo

Trả lời:

Giải bởi Vietjack

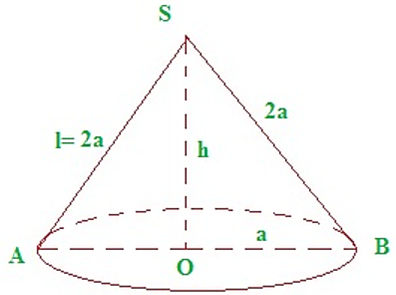
Một hình nón có thiết diện qua trục là một tam giác đều cạnh a. a) Tính diện tích xung quanh (ảnh 1)

Ta có: Độ dài đường sinh của hình nón là: l = SA = SB = 2a

Vì tam giác ABC đều, suy ra AB = SA = SB = 2a

Bán kính đường tròn đáy là: \(R = OA = \frac{{AB}}{2} = a\)

Vì tam giác SOB là tam giác vuông nên ta có:

Chiều cao của hình nó là:

\(h = SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)

a) Diện tích xung qunah của hình nón là:

S_xq = p.R.l = p.a.2a = 2pa² (đvdt)

Diện tích toàn phân của hình nón là:

S_tp = S_xq + S_đáy = 2pa² + pa² = 3pa² (đvdt)

b) Thể tích của hình nón là:

\(V = \frac{1}{3}S\,.\,h = \frac{1}{3}\pi {R^2}\,.\,h = \frac{1}{3}\pi {a^2}\,.\,a\sqrt 3 = \frac{{\pi {a^3}\sqrt 3 }}{3}\) (đvdt)

c) Diện tích của thiết diện chính là của tam giác SAB, ta có:

\({S_{SAB}} = \frac{1}{2}SO\,.\,AB = \frac{1}{2}\,.\,a\sqrt 3 \,.\,2a = {a^2}\sqrt 3 \) (đvdt)

Nhà sách VIETJACK:

Xem thêm kho sách »

Combo - Sổ tay kiên thức trọng tâm Toán, Lí, Hóa dành cho 2k7 VietJack

₫29.000 (Đã bán 152)

Sách - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 1,2k)

Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 1,6k)

Sách - Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 2,7k)

Bình luận hoặc Báo cáo
về câu hỏi!

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm nguyên hàm của hàm số f (x) = cos² (2x).

Xem đáp án » 11/07/2024 20,624

Câu 2:

Có bao nhiêu cách xếp 6 cặp vợ chồng ngồi xung quanh một chiếc bàn tròn, sao cho mỗi bà đều ngồi cạnh chồng của mình?

Xem đáp án » 11/07/2024 16,500

Câu 3:

Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

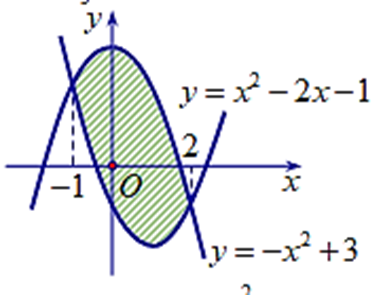
A. \(\int\limits_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} \);

B. \(\int\limits_{ - 1}^2 {\left( { - 2x + 2} \right)dx} \);

C. \(\int\limits_{ - 1}^2 {\left( {2x - 2} \right)dx} \);

D. \(\int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \).

Xem đáp án » 26/09/2023 9,624

Câu 4:

Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\) chứa điểm nào sau đây?

A. A(1; 2);

B. B(0; 2);

C. C(−1; 3);

D. \(D\left( {0;\; - \frac{1}{3}} \right)\).

Xem đáp án » 26/09/2023 8,943

Câu 5:

Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn 100°?

Xem đáp án » 11/07/2024 8,638

Câu 6:

Tính tổng các nghiệm nguyên của bất phương trình:

log₂ (x² + 3) − log₂ x + x² − 4x + 1 ≤ 0

Xem đáp án » 11/07/2024 7,441

Câu 7:

Trên mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(1; 3), B(−2; −2), C(3; 1). Tính cosin góc A của tam giác.

Xem đáp án » 11/07/2024 6,074

Xem thêm các câu hỏi khác »

Một hình nón có thiết diện qua trục là một tam giác đều cạnh a.

a) Tính diện tích xung quanh và diện tihcs toàn phần của hình nón

b) Tính thể tích của khối nón

c) Tính diệc tích của thiết diện

Nhà sách VIETJACK:

Tìm nguyên hàm của hàm số f (x) = cos² (2x).

Có bao nhiêu cách xếp 6 cặp vợ chồng ngồi xung quanh một chiếc bàn tròn, sao cho mỗi bà đều ngồi cạnh chồng của mình?

Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\) chứa điểm nào sau đây?

Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn 100°?

Tính tổng các nghiệm nguyên của bất phương trình:

log₂ (x² + 3) − log₂ x + x² − 4x + 1 ≤ 0

Trên mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(1; 3), B(−2; −2), C(3; 1). Tính cosin góc A của tam giác.

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

Một hình nón có thiết diện qua trục là một tam giác đều cạnh a. a) Tính diện tích xung quanh và diện tihcs toàn phần của hình nón b) Tính thể tích của khối nón c) Tính diệc tích của thiết diện

Nhà sách VIETJACK:

Tìm nguyên hàm của hàm số f (x) = cos2 (2x).

Có bao nhiêu cách xếp 6 cặp vợ chồng ngồi xung quanh một chiếc bàn tròn, sao cho mỗi bà đều ngồi cạnh chồng của mình?

Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\) chứa điểm nào sau đây?

Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn 100°?

Tính tổng các nghiệm nguyên của bất phương trình: log2 (x2 + 3) − log2 x + x2 − 4x + 1 ≤ 0

Trên mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(1; 3), B(−2; −2), C(3; 1). Tính cosin góc A của tam giác.

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Một hình nón có thiết diện qua trục là một tam giác đều cạnh a.

a) Tính diện tích xung quanh và diện tihcs toàn phần của hình nón

b) Tính thể tích của khối nón

c) Tính diệc tích của thiết diện

Tìm nguyên hàm của hàm số f (x) = cos² (2x).

Tính tổng các nghiệm nguyên của bất phương trình:

log₂ (x² + 3) − log₂ x + x² − 4x + 1 ≤ 0