Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD, M là trung điểm CD, I là điểm ở trên đoạn thẳng AG, BI cắt mặt phẳng (ACD) tại J. Khẳng định nào sau đây sai?
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD, M là trung điểm CD, I là điểm ở trên đoạn thẳng AG, BI cắt mặt phẳng (ACD) tại J. Khẳng định nào sau đây sai?
A. AM = (ACD) Ç (ABG);
B. A, J, M thẳng hàng;
C. J là trung điểm của AM;
D. DJ = (ACD) Ç (BDJ).
Quảng cáo
Trả lời:
Đáp án đúng là: C
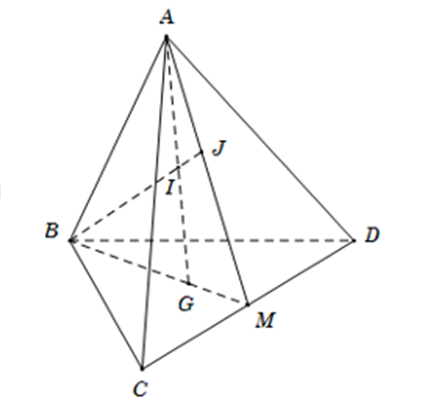
Ta có A là điểm chung thứ nhất giưuax hai mặt phẳng (ACD) và (GAB)
Do BG Ç CD = M
\( \Rightarrow \left\{ \begin{array}{l}M \in BG \subset \left( {ABG} \right) \Rightarrow M \in \left( {ABG} \right)\\M \in CD \subset \left( {ACD} \right) \Rightarrow M \in \left( {ACD} \right)\end{array} \right.\)
Suy ra M là điểm chung thứu hai giữa hai mặt phẳng (ACD) và (GAB)
Suy ra AM = (ACD) Ç (ABG) nên A đúng
Ta có: \(\left\{ \begin{array}{l}BI \subset \left( {ABG} \right)\\AM \subset \left( {ABM} \right)\\\left( {ABG} \right) \equiv \left( {ABM} \right)\end{array} \right.\)
Suy ra AM, BI đồng phẳng
Þ J = BI Ç AM
Suy ra A, J, M thẳng hàng nên B đúng
Ta có: \(\left\{ \begin{array}{l}DJ \subset \left( {ACD} \right)\\DJ \subset \left( {BDJ} \right)\end{array} \right. \Rightarrow DJ = \left( {ACD} \right) \cap \left( {BDJ} \right)\) nên D đúng
Điểm I di động trên AG nên J có thể không phải là trung điểm của AM nên C sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \[{\cos ^2}2x = \frac{{\cos 4x + 1}}{2} = \frac{1}{2}\cos 4x + \frac{1}{2}\]
Do đó nguyên hàm của hàm số f (x) = cos2 (2x) là:
\(\int {f\left( x \right)dx} = \int {\left( {\frac{1}{2}\cos 4x + \frac{1}{2}} \right)dx} = \frac{1}{8}\sin 4x + \frac{1}{2}x + C\).
Lời giải
Xếp 6 người chồng quanh bàn tròn có 5! cách.
Xếp các bà vợ vào ngồi cạnh chồng của mình, mỗi bà vợ có 2 vị trí ngồi nên có 26 cách.
Vậy số cách xếp là 5!.26 = 7680 cách.
Câu 3
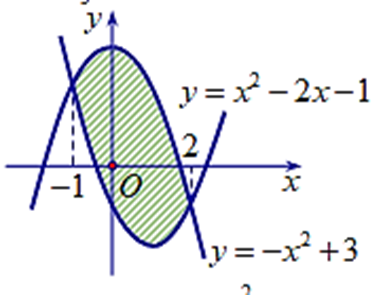
A. \(\int\limits_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} \);
B. \(\int\limits_{ - 1}^2 {\left( { - 2x + 2} \right)dx} \);
C. \(\int\limits_{ - 1}^2 {\left( {2x - 2} \right)dx} \);
D. \(\int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. A(1; 2);
B. B(0; 2);
C. C(−1; 3);
D. \(D\left( {0;\; - \frac{1}{3}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.