Câu hỏi:
26/09/2023 2,941
Một thầy giáo có 12 cuốn sách đôi một khác nhau, trong đó có 5 cuốn sách văn học, 4 cuốn sách âm nhạc và 3 cuốn sách hội họa. Thầy muốn lấy ra 6 cuốn và đem tặng cho 6 học sinh mỗi em một cuốn. Thầy giáo muốn rằng sau khi tặng xong, mỗi một trong 3 thể loại văn học, âm nhạc, hội họa đều còn lại ít nhất một cuốn. Hỏi thầy có tất cả bao nhiêu cách tặng?
Một thầy giáo có 12 cuốn sách đôi một khác nhau, trong đó có 5 cuốn sách văn học, 4 cuốn sách âm nhạc và 3 cuốn sách hội họa. Thầy muốn lấy ra 6 cuốn và đem tặng cho 6 học sinh mỗi em một cuốn. Thầy giáo muốn rằng sau khi tặng xong, mỗi một trong 3 thể loại văn học, âm nhạc, hội họa đều còn lại ít nhất một cuốn. Hỏi thầy có tất cả bao nhiêu cách tặng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Số cách lấy bằng số cách chọn ra 6 quyển để bỏ lại. Yêu cầu đặt ra là 6 quyển để lại phải đủ cả 3 môn.
TH1: 1 văn, 2 âm nhạc, 3 hội họa: \(C_5^1 \cdot C_4^2 \cdot C_3^3\)
TH2: 1 văn, 3 âm nhạc, 2 hội họa: \(C_5^1 \cdot C_4^3 \cdot C_3^2\)
TH3: 1 văn, 4 âm nhạc, 1 hội họa: \(C_5^1 \cdot C_4^4 \cdot C_3^1\)
TH4: 2 văn, 1 âm nhạc, 3 hội họa: \(C_5^2 \cdot C_4^1 \cdot C_3^3\)
TH5: 2 văn, 2 âm nhạc, 2 hội họa: \(C_5^2 \cdot C_4^2 \cdot C_3^2\)
TH6: 2 văn, 3 âm nhạc, 1 hội họa: \(C_5^2 \cdot C_4^3 \cdot C_3^1\)
TH7: 3 văn, 1 âm nhạc, 2 hội họa: \(C_5^3 \cdot C_4^1 \cdot C_3^2\)
TH8: 3 văn, 2 âm nhạc, 1 hội họa: \(C_5^3 \cdot C_4^2 \cdot C_3^1\)
TH9: 4 văn, 1 âm nhạc, 1 hội họa: \(C_5^4 \cdot C_4^1 \cdot C_3^1\)
Lấy 6 quyền sách chia cho 6 bạn: 6! = 720
Theo quy tắc nhân ta được 579 600 cách
Vậy đáp án cần chọn là D.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
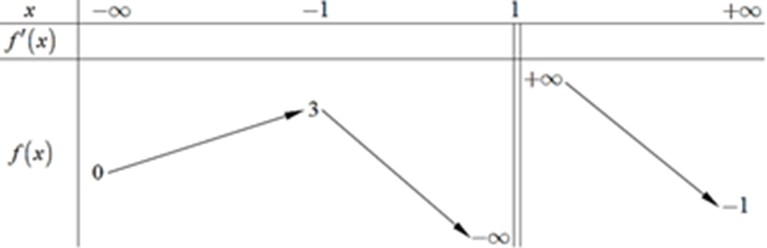
Ta có sô nghiệm của phương trình f(x) = m bằng số giao điềm của đồ thị hàm số y = f(x) và đường thẳng y = m
Do đó, dựa vào bàng biến thiên ta thấy, phương trình f(x) = m có 3 nghiệm phân biệt khi và chỉ khi 0 < m < 3
Kết hợp điều kiện \(m \in \mathbb{Z}\) suy ra \(m \in \{ 1;2\} \)
Do đó có 2 giá trị nguyên của tham số m thòa mãn yêu cầu bài toán
Vậy ta chọn đáp án D.
Lời giải
Đặt \(f(x) = {x^2} - 4x + m\)
Để phương trình có 2 nghiệm thỏa mãn \(0 < {x_1} < {x_2} < 3\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta ' > 0}\\{f(0) > 0}\\{f(3) > 0}\\{0 < \frac{S}{2} < 3}\end{array} \Leftrightarrow \left\{ \begin{array}{l}{4^2} - 4m > 0\\0 + m > 0\\{3^2} - 4.3 + m > 0\\0 < \frac{4}{2} < 3\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4 - m > 0}\\{m > 0}\\{m - 3 > 0}\\{0 < 2 < 3}\end{array} \Leftrightarrow 3 < m < 4} \right.} \right.\)
Vậy 3 < m < 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)