Câu hỏi:
13/07/2024 15,285
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y = x và y = –x + 2.
a) Vẽ hai đường thẳng đã cho trên cùng mặt phẳng tọa độ.
b) Tìm giao điểm A của hai đường thẳng đã cho.
c) Gọi B là giao điểm của đường thẳng y = –x + 2 và trục Ox. Chứng minh rằng tam giác OAB vuông tại A, tức hai đường thẳng y = x và y = –x + 2 vuông góc với nhau.
d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho?
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y = x và y = –x + 2.
a) Vẽ hai đường thẳng đã cho trên cùng mặt phẳng tọa độ.
b) Tìm giao điểm A của hai đường thẳng đã cho.
c) Gọi B là giao điểm của đường thẳng y = –x + 2 và trục Ox. Chứng minh rằng tam giác OAB vuông tại A, tức hai đường thẳng y = x và y = –x + 2 vuông góc với nhau.
d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a)
* Xét đường thẳng y = x
Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x.
Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1).
* Xét đường thẳng y = –x + 2
Cho y = 0 thì x = 2 nên điểm (2; 0) thuộc đường thẳng y = – x + 2.
Cho x = 0 thì y = 2 nên điểm (0; 2 ) thuộc đường thẳng y = –x + 2.
Đường thẳng y = – x + 2 đi qua hai điểm (2; 0) và (0; 2).
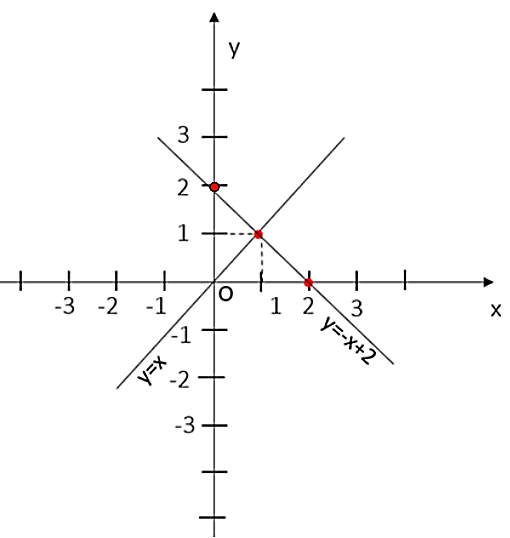
b) Phương trình hoành độ giao điểm của hai đường thẳng đã cho là:
x = –x + 2
Giải phương trình này ta được x = 1. Từ đó suy ra y = 1.
Vậy tọa độ giao điểm A(1; 1).
c) Giao điểm của đường thẳng y = –x + 2 và trục Ox là B(2; 0).
Gọi C là giao điểm của đường thẳng y = –x + 2 và trục Oy. Suy ra C(0; 2).
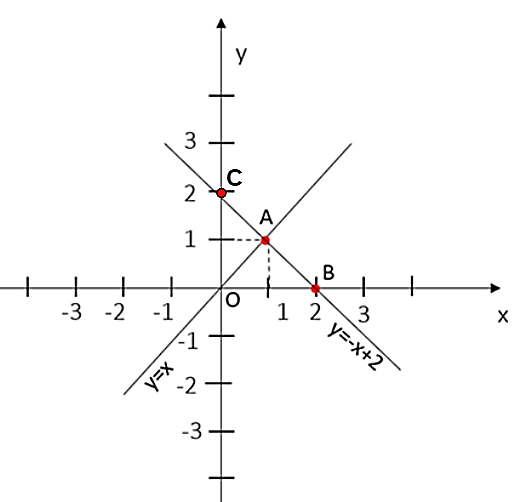
Dễ thấy tam giác OBC vuông cân tại O (vì OB = OC = 2).
Xét hai tam giác OAB và OAC có:
Cạnh OA chung;
OB = OC;
=
Do đó ΔOAB = ΔOAC, từ đó suy ra AB = AC.
Điều này chứng tỏ A là trung điểm của BC, mà ΔOBC cân tại O nên OA ⊥ AB, tức là ΔOAB vuông tại A.
d) Đường thẳng y = x có hệ số góc bằng 1.
Đường thẳng y = – x + 1 có hệ số góc bằng –1.
Tích của hai hệ số góc của hai đường thẳng đã cho bằng –1.
Từ câu c), ta có nhận xét:
Hai đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng –1.Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi hàm số cần tìm là y = ax + b (a ≠ 0).
Vì đồ thị hàm số là đường thẳng có hệ số góc bằng 3 nên a = 3 hay y = 3x + b.
Hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1; –2) , thay x = 1, y = –2 vào công thức hàm số, ta được:
– 2 = 3 . 1 + b, tức là b = – 5.
Vậy ta có hàm số là y = 3x – 5.
Lời giải
Gọi y = ax + b là hàm số cần tìm (a ≠ 0).
Vì đồ thị của hàm số song song với đường thẳng y = –3x + 1 nên a = –3 và b ≠ 1.
Suy ra y = – 3x + 1 (b ≠ 1).
Lại có, đồ thị hàm số là đường thẳng đi qua điểm (2; 6) nên ta có:
6 = –3 . 2 + b, suy ra b = 12 (thỏa mãn điều kiện b ≠ 1).
Vậy hàm số cần tìm là y = –3x + 12.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận