Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Quảng cáo
Trả lời:
Theo đề có AB ^ (P) và AC ^ (P).
Mà có duy nhất một đường thẳng đi qua A và vuông góc với (P) nên AB và AC trùng nhau. Do đó A, B, C thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
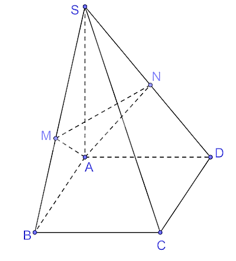
- Vì SA ^ (ABCD) nên SA ^ BC.
Do ABCD là hình chữ nhật nên BC ^ AB mà SA ^ BC nên BC ^ (SAB), suy ra BC ^ AM.
Lại có, M là hình chiếu của A trên SB nên AM ^ SB.
Vì AM ^ SB và BC ^ AM nên AM ^ (SBC).
- Vì SA ^ (ABCD) nên SA ^ CD.
Do ABCD là hình chữ nhật nên AD ^ CD.
Vì AD ^ CD và SA ^ CD nên CD ^ (SAD), suy ra CD ^ AN.
Do N là hình chiếu của A trên SD nên AN ^ SD.
Vì AN ^ SD và CD ^ AN nên AN ^ (SCD).
- Do AM ^ (SBC) nên AM ^ SC và AN ^ (SCD) nên AN ^ SC.
Vì AM ^ SC và AN ^ SC nên SC ^ (AMN).
Lời giải
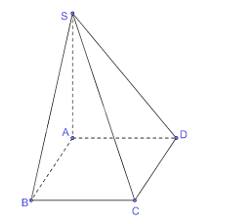
Vì SA ^ (ABCD) nên SA ^ AD, SA ^ AB, SA ^ BC, SA ^ CD.
Do ABCD là hình chữ nhật nên AB ^ BC, AD ^ DC.
Vì SA ^ AB nên tam giác SAB vuông tại A.
Vì SA ^ AD nên tam giác SAD vuông tại A.
Vì SA ^ BC và AB ^ BC nên BC ^ (SAB), suy ra BC ^ SB hay tam giác SBC vuông tại B.
Vì SA ^ CD và AD ^ DC nên CD ^ (SAD), suy ra CD ^ SD hay tam giác SCD vuông tại D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.