Cho tam giác ABC có đường cao AH. Lấy các điểm E, F lần lượt trên AB, AC sao cho HE, HF lần lượt vuông góc với AB, AC. Lấy điểm D trên EF sao cho AD vuông góc với EF. Đường thẳng AD cắt BC tại M. Chứng minh rằng:
a) AE . AB = AF . AC.
b) ∆ADE ᔕ ∆AHC và ∆ANF ᔕ ∆AMB.
Cho tam giác ABC có đường cao AH. Lấy các điểm E, F lần lượt trên AB, AC sao cho HE, HF lần lượt vuông góc với AB, AC. Lấy điểm D trên EF sao cho AD vuông góc với EF. Đường thẳng AD cắt BC tại M. Chứng minh rằng:
a) AE . AB = AF . AC.
b) ∆ADE ᔕ ∆AHC và ∆ANF ᔕ ∆AMB.
Câu hỏi trong đề: Giải SBT Toán 8 KNTT Bài tập ôn tập cuối năm có đáp án !!
Quảng cáo
Trả lời:
Lời giải
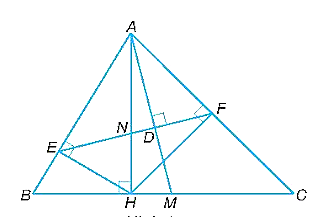
a) Vì AH là đường cao của tam giác ABC nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \).
Vì HE, HF vuông góc với AB, AC nên ta có:
\(\widehat {HEB} = \widehat {HEA} = \widehat {HFA} = \widehat {HFC} = 90^\circ \).
Tam giác HEA và tam giác BHA có:
\(\widehat {HEA} = \widehat {AHB} = 90^\circ \)
\(\widehat {BAH}\) chung
Do đó, ∆HEA ᔕ ∆BHA (g.g).
Suy ra \(\frac{{AE}}{{AH}} = \frac{{AH}}{{AB}}\) nên AE . AB = AH2 (1).
Tam giác HFA và tam giác CHA có:
\(\widehat {HFA} = \widehat {AHC} = 90^\circ \)
\(\widehat {CAH}\) chung
Do đó, ∆HFA ᔕ ∆CHA (g.g).
Suy ra \(\frac{{AF}}{{AH}} = \frac{{AH}}{{AC}}\) nên AF . AC = AH2 (2).
Từ (1) và (2) suy ra AE . AB = AF . AC.
b) Vì AE . AB = AF . AC nên \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\).
Tam giác AEF và tam giác ACB có:
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\)
\(\widehat {BAC}\) chung
Do đó, ∆AEF ᔕ ∆ACB (c.g.c).
Suy ra \(\widehat {AEF} = \widehat C\).
Tam giác AED và tam giác ACH có:
\(\widehat {ADE} = \widehat {AHC} = 90^\circ \)
\(\widehat {AEF} = \widehat C\) (cmt)
Do đó, ∆ADE ᔕ ∆AHC (g.g).
Suy ra \(\widehat {EAD} = \widehat {CAH}\).
Do đó, \(\widehat {NAF} = \widehat {CAH} = \widehat {EAD} = \widehat {MAB}\).
Hai tam giác ANF và AMB có:
\(\widehat {NAF} = \widehat {MAB}\) (chứng minh trên)
\(\widehat {AFN} = \widehat {AFE} = \widehat {ABC} = \widehat {ABM}\) (do ∆AEF ᔕ ∆ACB)
Do đó ∆ANF ᔕ ∆AMB (g.g).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
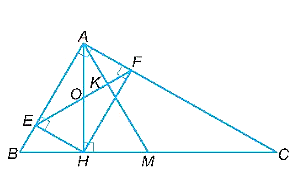
a)Vì tam giác ABC vuông tại A nên \(\widehat {BAC} = 90^\circ \).
Vì E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC nên HE vuông góc với AB, HF vuông góc với AC.
Do đó, \(\widehat {HEB} = \widehat {HEA} = \widehat {HFA} = \widehat {HFC} = 90^\circ \).
Xét tứ giác AFHE có: \(\widehat {BAC} = \widehat {HEA} = \widehat {HFA} = 90^\circ \).
Do đó, tứ giác AFHE là hình chữ nhật.
Suy ra AH = FE (hai đường chéo bằng nhau).
b) Vì tứ giác AFHE là hình chữ nhật nên \(\widehat {FHE} = 90^\circ \).
Vì AM là đường trung tuyến trong tam giác ABC vuông tại A nên
AM = MB = MC = \(\frac{1}{2}BC\).
Tam giác AMB có AM = MB nên tam giác AMB cân tại M.
Do đó, \(\widehat {MAB} = \widehat B\).
Lại có \(\widehat B = \widehat {AHE}\,\,\,\,\,\left( { = 90^\circ - \widehat {HEB}} \right)\).
Nên \(\widehat {MAB} = \widehat {AHE}\) (1).
Gọi O là giao điểm của hai đường chéo FE và AH của hình chữ nhật AFHE.
Do đó, OH = OE = OF = OA.
Tam giác OAE có OA = OE nên tam giác OAE cân tại O.
Suy ra \(\widehat {OEA} = \widehat {OAE}\).
Mà AE song song với FH (do AFHE là hình chữ nhật) nên \(\widehat {OHF} = \widehat {OAE}\) (hai góc so le trong).
Do đó, \(\widehat {OEA} = \widehat {OHF}\) (2).
Lại có \(\widehat {OHF} + \widehat {OHE} = \widehat {FHE} = 90^\circ \) (3).
Từ (1), (2), (3) ta có: \[\widehat {MAB} + \widehat {OEA} = 90^\circ \].
Gọi K là giao điểm của AM và EF. Khi đó, \[\widehat {KAE} + \widehat {KEA} = 90^\circ \]. Suy ra \(\widehat {AKE} = 90^\circ \).
Vậy AM vuông góc với EF tại K.
Lời giải
Lời giải
a) Hàm số y = (3m + 1)x – 2m là hàm số bậc nhất khi 3m + 1 ≠ 0, tức là m ≠ \(\frac{{ - 1}}{3}\).
b) Vì đồ thị hàm số đã cho là đường thẳng song song với đường thẳng y = –2x + 5 nên
3m + 1 = –2 và –2m ≠ 5.
Tức là m = –1 và m ≠ \(\frac{{ - 5}}{2}\). Suy ra m = – 1.
Vậy m = – 1.
c) Với m = –1, ta có y = –2x + 2.
Đồ thị hàm số y = –2x + 2 là đường thẳng đi qua hai điểm A(0; 2), B(1; 0) như hình dưới đây.
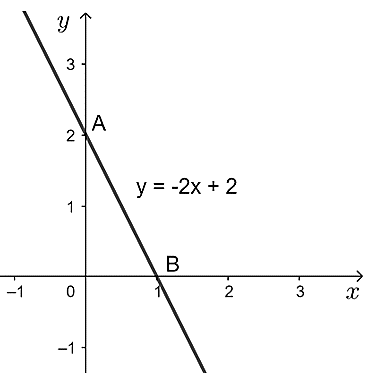
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.