Câu hỏi:
11/07/2024 1,866
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 10 cm, cạnh bên SD = 15 cm. Gọi O là giao điểm của AC và BD, M và N lần lượt là trung điểm của AB và CD.
a) Chứng minh SO ⊥ MN. Từ đó tính độ dài đường cao SO của hình chóp.
b) Tính thể tích của hình chóp.
c) Tính diện tích toàn phần của hình chóp.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 10 cm, cạnh bên SD = 15 cm. Gọi O là giao điểm của AC và BD, M và N lần lượt là trung điểm của AB và CD.
a) Chứng minh SO ⊥ MN. Từ đó tính độ dài đường cao SO của hình chóp.
b) Tính thể tích của hình chóp.
c) Tính diện tích toàn phần của hình chóp.
Câu hỏi trong đề: Giải SBT Toán 8 KNTT Bài tập ôn tập cuối năm có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
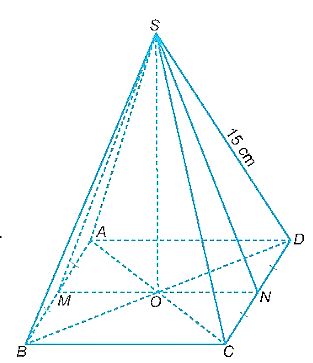
a) Vì các mặt bên của hình chóp tứ giác đều là các tam giác cân bằng nhau nên các đường trung tuyến tương ứng của chúng bằng nhau, tức là SM = SN.
Do đó, tam giác SMN là tam giác cân tại S và O là trung điểm của MN nên SO ⊥ MN.
(Vì M và N lần lượt là trung điểm của AB và CD trong hình vuông ABCD với O là giao điểm của hai đường chéo nên ta chứng minh được O là trung điểm của MN).
Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore ta có:
AC2 = AB2 + BC2 = 102 + 102 = 200 nên AC = \(10\sqrt 2 \) cm.
Do đó, BD = AC = \(10\sqrt 2 \) cm, suy ra DO = \(\frac{1}{2}\)BD = \(5\sqrt 2 \) cm.
Xét tam giác SOD vuông tại O, áp dụng định lý Pythagore ta có:
DO2 + SO2 = SD2
Suy ra SO2 = SD2 – DO2 = 152 – \({\left( {5\sqrt 2 } \right)^2}\) = 175.
Nên SO = \(\sqrt {175} = 5\sqrt 7 \) cm.
b) Thể tích của hình chóp tứ giác đều S.ABCD là:
\({V_{S.ABCD}} = \frac{1}{3} \cdot SO \cdot {S_{ABCD}} = \frac{1}{3} \cdot 5\sqrt 7 \cdot {10^2} = \frac{{500\sqrt 7 }}{3}\) (cm3).
c) Ta có SM là trung tuyến trong tam giác cân SAB nên SM đồng thời là đường cao.
Do đó, SM là một trung đoạn của hình chóp tứ giác đều.
Ta có SA = SD = 15 cm, AM = \(\frac{1}{2}\)AB = 5 cm.
Xét tam giác SMA vuông tại M, áp dụng định lý Pythagore ta có:
SM2 + AM2 = SA2
Do đó, SM2 = SA2 – AM2 = 152 – 52 = 200 nên SM = \(10\sqrt 2 \) cm.
Nửa chu vi đáy ABCD là: p = 10 . 4 : 2 = 20 cm.
Diện tích xung quanh của hình chóp là:
\({S_{xq}} = SM \cdot p = 10\sqrt 2 \cdot 20 = 200\sqrt 2 \) (cm2).
Diện tích đáy ABCD là: SABCD = 102 = 100 (cm2).
Diện tích toàn phần của hình chóp S.ABCD là:
\({S_{tp}} = {S_{xq}} + {S_{ABCD}} = 200\sqrt 2 + 100 = 100\left( {2\sqrt 2 + 1} \right)\) (cm2).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
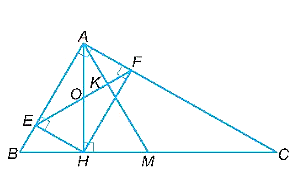
a)Vì tam giác ABC vuông tại A nên \(\widehat {BAC} = 90^\circ \).
Vì E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC nên HE vuông góc với AB, HF vuông góc với AC.
Do đó, \(\widehat {HEB} = \widehat {HEA} = \widehat {HFA} = \widehat {HFC} = 90^\circ \).
Xét tứ giác AFHE có: \(\widehat {BAC} = \widehat {HEA} = \widehat {HFA} = 90^\circ \).
Do đó, tứ giác AFHE là hình chữ nhật.
Suy ra AH = FE (hai đường chéo bằng nhau).
b) Vì tứ giác AFHE là hình chữ nhật nên \(\widehat {FHE} = 90^\circ \).
Vì AM là đường trung tuyến trong tam giác ABC vuông tại A nên
AM = MB = MC = \(\frac{1}{2}BC\).
Tam giác AMB có AM = MB nên tam giác AMB cân tại M.
Do đó, \(\widehat {MAB} = \widehat B\).
Lại có \(\widehat B = \widehat {AHE}\,\,\,\,\,\left( { = 90^\circ - \widehat {HEB}} \right)\).
Nên \(\widehat {MAB} = \widehat {AHE}\) (1).
Gọi O là giao điểm của hai đường chéo FE và AH của hình chữ nhật AFHE.
Do đó, OH = OE = OF = OA.
Tam giác OAE có OA = OE nên tam giác OAE cân tại O.
Suy ra \(\widehat {OEA} = \widehat {OAE}\).
Mà AE song song với FH (do AFHE là hình chữ nhật) nên \(\widehat {OHF} = \widehat {OAE}\) (hai góc so le trong).
Do đó, \(\widehat {OEA} = \widehat {OHF}\) (2).
Lại có \(\widehat {OHF} + \widehat {OHE} = \widehat {FHE} = 90^\circ \) (3).
Từ (1), (2), (3) ta có: \[\widehat {MAB} + \widehat {OEA} = 90^\circ \].
Gọi K là giao điểm của AM và EF. Khi đó, \[\widehat {KAE} + \widehat {KEA} = 90^\circ \]. Suy ra \(\widehat {AKE} = 90^\circ \).
Vậy AM vuông góc với EF tại K.
Lời giải
Lời giải
a) Hàm số y = (3m + 1)x – 2m là hàm số bậc nhất khi 3m + 1 ≠ 0, tức là m ≠ \(\frac{{ - 1}}{3}\).
b) Vì đồ thị hàm số đã cho là đường thẳng song song với đường thẳng y = –2x + 5 nên
3m + 1 = –2 và –2m ≠ 5.
Tức là m = –1 và m ≠ \(\frac{{ - 5}}{2}\). Suy ra m = – 1.
Vậy m = – 1.
c) Với m = –1, ta có y = –2x + 2.
Đồ thị hàm số y = –2x + 2 là đường thẳng đi qua hai điểm A(0; 2), B(1; 0) như hình dưới đây.
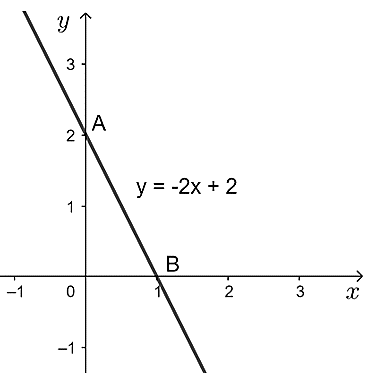
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận