Câu hỏi:
13/07/2024 827
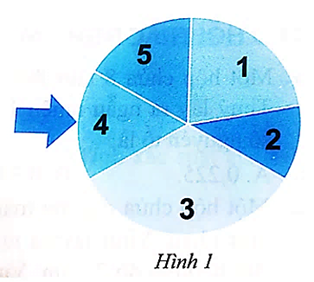
Cho tấm bìa như Hình 1. Thu xoay tấm bìa quanh tâm của nó và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào.
Kết quả sau 150 lần xoay được ghi lại ở bảng sau.
Ô số
1
2
3
4
5
Số lần
36
12
54
27
21
Hãy tính xác suất thực nghiệm của các biến cố:
A: “Mũi tên chỉ vào ô ghi số 1”;
B: “Mũi tẻn chì vào ô ghi số chẵn”;
C: “Mũi tên chỉ vào ô ghi số lớn hơn 3”;
Kết quả sau 150 lần xoay được ghi lại ở bảng sau.
|
Ô số |
1 |
2 |
3 |
4 |
5 |
|
Số lần |
36 |
12 |
54 |
27 |
21 |
Hãy tính xác suất thực nghiệm của các biến cố:
A: “Mũi tên chỉ vào ô ghi số 1”;
B: “Mũi tẻn chì vào ô ghi số chẵn”;
C: “Mũi tên chỉ vào ô ghi số lớn hơn 3”;
Quảng cáo
Trả lời:
Giải bởi Vietjack
• Số lần xảy ra biến cố A là 36.
Xác suất thực nghiệm của biến cố A là: \(P\left( A \right) = \frac{{36}}{{150}} = 0,24\).
• Số lần xảy ra biến cố B là 12 + 27 = 39 (lần).
Xác suất thực nghiệm của biến cố B là: \(P\left( B \right) = \frac{{39}}{{150}} = 0,26\).
• Số lần xảy ra biến cố C là 27 + 21 = 48 (lần).
Xác suất thực nghiệm của biến cố C là: \(P\left( C \right) = \frac{{48}}{{150}} = 0,32\).
Vậy xác suất thực nghiệm của các biến cố A là 0,24; xác suất thực nghiệm của các biến cố B là 0,26 và xác suất thực nghiệm của các biến cố là 0,32.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi n là số quả bóng trong bình.
Xác suất thực nghiệm của biến cố “Lấy được quả bóng ghi số có một chữ số” là:
\(\frac{{40}}{{200}} = 0,2\).
Các trường hợp xảy ra của biến cố “Lấy được quả bóng ghi số có một chữ số” là quả bóng lấy ra chứa một trong các số 1; 2; 3; 4; 5; 6; 7; 8; 9.
Xác suất lý thuyết của biến cố “Lấy được quả bóng ghi số có một chữ số” là \(\frac{9}{n}\).
Vì số phép thử lớn nên xác suất thực nghiệm và xác suất lý thuyết của biến cố “Lấy được quả bóng ghi số có một chữ số” là gần bằng nhau nên ta có
\(\frac{9}{n} \approx 0,2\), tức là \(n \approx \frac{9}{{0,2}} = 45\).
Vậy trong bình có khoảng 45 quả bóng.
Lời giải
Xác suất thực nghiệm của biến cố “Lấy được tấm thẻ màu đỏ” là \(\frac{{40}}{{120}} = \frac{1}{3}\).
Gọi số tấm thẻ màu đỏ trong hộp là n. Tổng số thẻ trong hộp là n + 7.
Xác suất lý thuyết của biến cố “Lấy được tấm thẻ màu đỏ” là \(\frac{7}{{n + 7}}\).
Vì số phép thử lớn nên xác suất thực nghiệm và xác suất lý thuyết của biến cố “Lấy được tấm thẻ màu đỏ” là gần bằng nhau nên ta có:
\(\frac{7}{{n + 7}} \approx \frac{1}{3}\), tức là n + 7 ≈ 21 hay n ≈ 14.
Vậy có khoảng 14 tấm thẻ màu vàng trong hộp.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án