Cho tam giác ABC cân tại A, AB = AC = m, BC = n. Đường phân giác góc B cắt AC tại I, đường phân giác góc C cắt AB tại H. Khẳng định nào sau đây là đúng?
Cho tam giác ABC cân tại A, AB = AC = m, BC = n. Đường phân giác góc B cắt AC tại I, đường phân giác góc C cắt AB tại H. Khẳng định nào sau đây là đúng?
A. \({\rm{HI}} = \frac{{{\rm{m}} - {\rm{n}}}}{{{\rm{m + n}}}}\);
B. \({\rm{HI}} = \frac{{{\rm{m + n}}}}{{{\rm{m}} \cdot {\rm{n}}}}\);
C. \({\rm{HI}} = \frac{{{\rm{mn}}}}{{{\rm{m + n}}}}\);
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
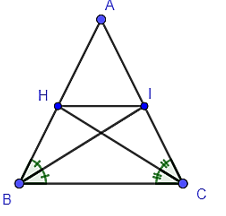
Tam giác ABC có:
+ BI là đường phân giác của góc B.
Do đó ta có: \(\frac{{{\rm{AI}}}}{{{\rm{IC}}}} = \frac{{{\rm{AB}}}}{{{\rm{BC}}}}\) hay \(\frac{{{\rm{AI}}}}{{{\rm{IC}}}} = \frac{{\rm{m}}}{{\rm{n}}}\)(1).
+ CH là đường phân giác của góc C.
Do đó ta có: \(\frac{{{\rm{AH}}}}{{{\rm{HB}}}} = \frac{{{\rm{AC}}}}{{{\rm{BC}}}}\) hay \(\frac{{{\rm{AH}}}}{{{\rm{HB}}}} = \frac{{\rm{m}}}{{\rm{n}}}\)(2).
Từ (1) và (2) suy ra \(\frac{{{\rm{AH}}}}{{{\rm{HB}}}} = \frac{{{\rm{AI}}}}{{{\rm{IC}}}} = \frac{{\rm{m}}}{{\rm{n}}}\).
Theo định lí Thalès đảo ta suy ra HI // BC.
Theo (2) ta có \(\frac{{{\rm{AH}}}}{{{\rm{HB}}}} = \frac{{\rm{m}}}{{\rm{n}}}\) nên \(\frac{{{\rm{AH + HB}}}}{{{\rm{HB}}}} = \frac{{{\rm{m + n}}}}{{\rm{n}}}\) hay \(\frac{{{\rm{AB}}}}{{{\rm{HB}}}} = \frac{{{\rm{m + n}}}}{{\rm{n}}}\).
Suy ra \(\frac{{{\rm{HB}}}}{{{\rm{AB}}}} = \frac{{\rm{n}}}{{{\rm{m + n}}}}\), khi đó, \(\frac{{{\rm{HA}}}}{{{\rm{AB}}}} = \frac{{AB - HB}}{{AB}} = 1 - \frac{{HB}}{{AB}} = \frac{{\rm{m}}}{{{\rm{m + n}}}}\).
Vì HI // BC nên ta có: \(\frac{{{\rm{AH}}}}{{{\rm{AB}}}} = \frac{{{\rm{HI}}}}{{{\rm{BC}}}}\).
Suy ra \({\rm{HI}} = \frac{{{\rm{AH}}}}{{{\rm{AB}}}} \cdot {\rm{BC = }}\frac{{\rm{m}}}{{{\rm{m + n}}}} \cdot {\rm{n}} = \frac{{{\rm{mn}}}}{{{\rm{m + n}}}}\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\frac{5}{8}\);
B. \(\frac{5}{9}\);
C. \(\frac{8}{5}\);
D. \(\frac{9}{8}\).
Lời giải
Đáp án đúng là: A
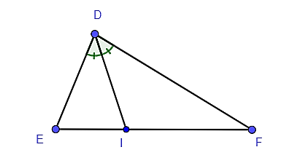
Tam giác DEF có DI là đường phân giác của góc D.
Do đó ta có: \(\frac{{{\rm{DE}}}}{{{\rm{DF}}}} = \frac{{{\rm{EI}}}}{{{\rm{IF}}}}\) hay \(\frac{{{\rm{EI}}}}{{{\rm{IF}}}} = \frac{5}{8}\).
Tỉ số diện tích của tam giác DEI và DFI chính là tỉ số \(\frac{{{\rm{EI}}}}{{{\rm{IF}}}}\) (vì hai tam giác này có chung đường cao hạ từ D đến EF).
Vậy tỉ số diện tích của tam giác DEI và tam giác DFI là \(\frac{5}{8}\).
Câu 2
A. \(\frac{{19}}{3}\);
B. \(\frac{9}{{13}}\);
C. \(\frac{5}{{13}}\);
D. \(\frac{{13}}{{19}}\).
Lời giải
Đáp án đúng là: B
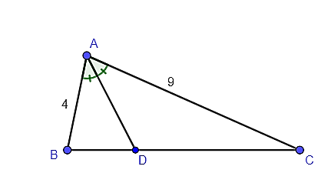
Tam giác ABC có AD là đường phân giác của góc A.
Do đó ta có \(\frac{{{\rm{AB}}}}{{{\rm{AC}}}} = \frac{{{\rm{BD}}}}{{{\rm{DC}}}}\) hay \(\frac{6}{7} = \frac{{\rm{x}}}{{\rm{y}}}\)
Suy ra \({\rm{x}} = \frac{6}{7}{\rm{y}}\).
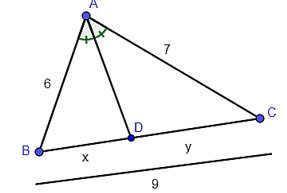
Ta có BD + DC = BC hay x + y = 9.
Từ đó ta có \(\frac{6}{7}{\rm{y}} + {\rm{y}} = 9\), suy ra \(\frac{{13}}{7}{\rm{y}} = 9\).
Vậy \({\rm{y}} = \frac{{63}}{{13}}\) và \({\rm{x}} = \frac{{54}}{{13}}\).
Do đó \({\rm{y}} - {\rm{x}} = \frac{{63}}{{13}} - \frac{{54}}{{13}} = \frac{9}{{13}}\).
Câu 3
A. \(\frac{4}{9}\);
B. \(\frac{9}{4}\);
C. \(\frac{1}{4}\);
D. \(\frac{1}{9}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập