Câu hỏi:

13/07/2024 11,887

Kính viễn vọng không gian Hubble được triển khai vào ngày 24 tháng 4 năm 1990, bởi tàu con thoi Discovery. Vận tốc của tàu con thoi trong nhiệm vụ này từ khi xuất phát tại t = 0 (s) cho đến khi tên lửa đẩy nhiên liệu rắn bị loại bỏ ở t = 126 (s) được xác định theo phương trình sau:

v(t) = 0,001302t³ – 0,09029t² + 23,61t – 3,083 (ft/s).

(Nguồn: James Stewart, Calculus)

Tính gia tốc tức thời của tàu con thoi trên tại thời điểm t = 100 (s) (làm tròn kết quả đến hàng phần nghìn).

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 11 Cánh diều Bài tập cuối chương 7 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gia tốc tức thời của tàu con thoi tại thời điểm t (s) là:

a(t) = v’(t)

= (0,001302t³ – 0,09029t² + 23,61t – 3,083)’

= 0,003906t² – 0,18058t + 23,61 (ft/s²).

Gia tốc tức thời của tàu con thoi tại thời điểm t = 100 (s) là:

a(100) = 0,003906.100² – 0,18058.100 + 23,61 = 44,612 (ft/s²).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số $f (x) = sin \frac{x}{2} cos \frac{x}{2} .$ Khi đó, f’(x) bằng:

Xem đáp án

Lời giải

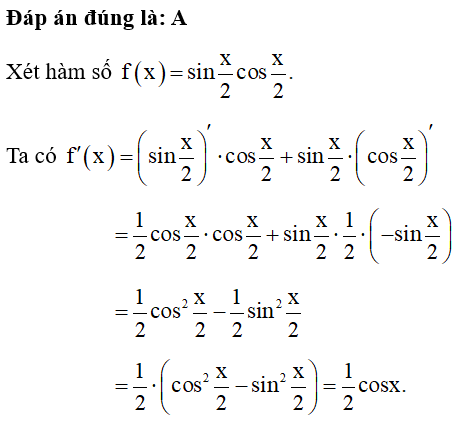
Cho hàm số f(x)= sin x/2 cos x/2 . Khi đó, f’(x) bằng: (ảnh 1)

Câu 2

Một chất điểm có phương trình chuyển động $s (t) = 2 sin (6 t + \frac{π}{4}),$ trong đó t > 0, t tính bằng giây, s(t) tính bằng centimét. Tính vận tốc tức thời và gia tốc tức thời của chất điểm tại thời điểm $t = \frac{π}{4} (s) .$

Xem đáp án

Lời giải

Một chất điểm có phương trình chuyển động s(t)= 2sin( 6t + pi/4) trong đó t > 0, t tính bằng giây, s(t) tính bằng centimét. Tính vận tốc tức thời và gia tốc tức thời của chất điểm tại thời điểm (ảnh 1)

Câu 3

Cho hàm số $f (x) = \frac{2 x - 3}{x + 4}$ có đồ thị (C).

a) Tìm đạo hàm của hàm số.

b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng –3.

c) Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Sau khi uống đồ uống có cồn, nồng độ cồn trong máu tăng lên rồi giảm dần được xác định bằng hàm số C(t) =1,35te^–2^,^802t, trong đó C (mg/ml) là nồng độ cồn, t (h) là thời điểm đo tính từ ngay sau khi uống 15 ml đồ uống có cồn.

(Nguồn: P. Wilkinson et al., Pharmacokinetics of Ethanol after Oral Administration in the Fasting State, 1977)

Giả sử một người uống hết nhanh 15 ml đồ uống có cồn. Tính tốc độ chuyển hoá nồng độ cồn trong máu của người đó tại thời điểm t = 3 (h) (làm tròn kết quả đến hàng phần triệu).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số $f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 12 x .$

a) Tìm f’(x) và giải bất phương trình f’(x) > 0.

b) Tìm f’’(x) và giải phương trình f’’(x) = 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số f(x) = loga(bx). Khi đó, f’(x) bằng:

A. $\frac{1}{b x} .$

B. $\frac{1}{a x} .$

C. $\frac{1}{x ln a} .$

D. $\frac{1}{x ln b} .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Cho hàm số fx=sinx2cosx2. Khi đó, f’(x) bằng:

Một chất điểm có phương trình chuyển động st=2sin6t+π4, trong đó t > 0, t tính bằng giây, s(t) tính bằng centimét. Tính vận tốc tức thời và gia tốc tức thời của chất điểm tại thời điểm t=π4 s.

Cho hàm số fx=2x−3x+4 có đồ thị (C). a) Tìm đạo hàm của hàm số. b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng –3. c) Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 1.

Cho hàm số fx=13x3−12x2−12x. a) Tìm f’(x) và giải bất phương trình f’(x) > 0. b) Tìm f’’(x) và giải phương trình f’’(x) = 0.

Cho hàm số f(x) = loga(bx). Khi đó, f’(x) bằng: A. 1bx. B. 1ax. C. 1xlna. D. 1xlnb.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số $f (x) = sin \frac{x}{2} cos \frac{x}{2} .$ Khi đó, f’(x) bằng:

Một chất điểm có phương trình chuyển động $s (t) = 2 sin (6 t + \frac{π}{4}),$ trong đó t > 0, t tính bằng giây, s(t) tính bằng centimét. Tính vận tốc tức thời và gia tốc tức thời của chất điểm tại thời điểm $t = \frac{π}{4} (s) .$

Cho hàm số $f (x) = \frac{2 x - 3}{x + 4}$ có đồ thị (C).

a) Tìm đạo hàm của hàm số.

b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng –3.

c) Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 1.

Cho hàm số $f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 12 x .$

a) Tìm f’(x) và giải bất phương trình f’(x) > 0.

b) Tìm f’’(x) và giải phương trình f’’(x) = 0.

Cho hàm số f(x) = loga(bx). Khi đó, f’(x) bằng:

A. $\frac{1}{b x} .$

B. $\frac{1}{a x} .$

C. $\frac{1}{x ln a} .$

D. $\frac{1}{x ln b} .$