Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam giác đồng dạng?
Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam giác đồng dạng?
A. 4;
B. 6;
C. 8;
Quảng cáo
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: D
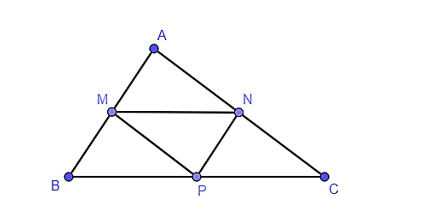
Vì M, N lần lượt là trung điểm của AB, AC.
Suy ra MN là đường trung bình của tam giác ABC nên MN // BC.
Vì M, P lần lượt là trung điểm của AB, BC.
Suy ra MP là đường trung bình của tam giác ABC nên MP // AC.
Vì N, P lần lượt là trung điểm của AC, BC.
Suy ra NP là đường trung bình của tam giác ABC nên NP // AB.
Xét tam giác ABC:
+ Do MN // BC nên ΔAMN ᔕ ΔABC.
+ Do MP // AC nên ΔMBP ᔕ ΔABC.
+ Do NP // AB nên ΔNPC ᔕ ΔABC.
Vì ΔAMN ᔕ ΔABC, ΔMBP ᔕ ΔABC, ΔNPC ᔕ ΔABC nên các tam giác AMN, MBP, NPC đôi một đồng dạng với nhau.
Xét hai tam giác AMN và PNM có:
AM = PN
MN: Cạnh chung
MP = AN
Suy ra ΔAMN = ΔPNM (c – c – c).
Do đó, ΔAMN ᔕ ΔPNM.
Từ đó suy ra 5 tam giác AMN, PNM, MBP, NPC, ABC đôi một đồng dạng với nhau.
Vậy có tất cả 10 cặp tam giác đồng dạng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
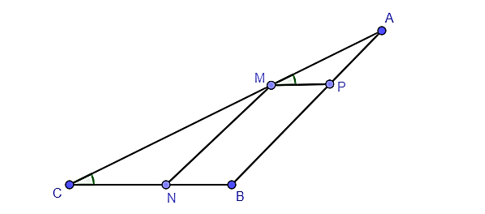
A. ΔAMP ᔕ ΔACB;
B. ΔMCN ᔕ ΔACB;
C. ΔAMP ᔕ ΔMCN;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
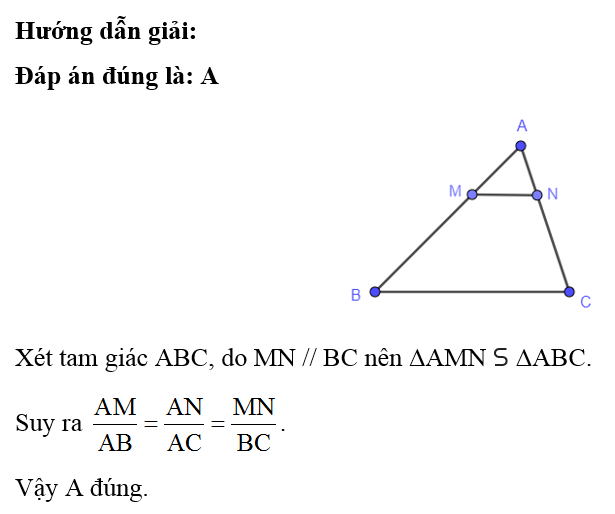
Xét tam giác ABC, do MN // AB nên ΔMCN ᔕ ΔACB.
Lại có mà hai góc này ở vị trí đồng vị nên MP // CB.
Xét tam giác ABC, do MP // CB nên ΔAMP ᔕ ΔACB.
Vì ΔMCN ᔕ ΔACB, ΔAMP ᔕ ΔACB nên ΔAMP ᔕ ΔMCN.
Vậy D sai.
Lời giải
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
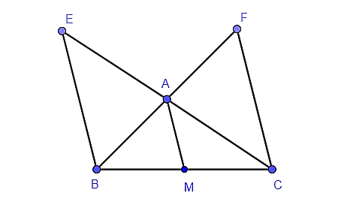
A. Tam giác FAD;
B. Tam giác DCE;
C. Cả A, B đều sai;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
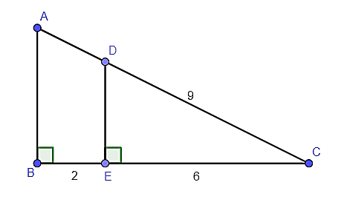
A. ΔCAB ᔕ ΔCDE với tỉ số đồng dạng ;
B. ΔABC ᔕ ΔDEC với tỉ số đồng dạng ;
C. ΔDEC ᔕ ΔBAC với tỉ số đồng dạng ;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.