Câu hỏi:
29/01/2024 415
Cho hình vuông ABCD cạnh a. Lấy M thuộc AB, N thuộc AD sao cho AM + AN + MN = 2a. Chứng minh \(\widehat {MCN} = 45^\circ \).
Cho hình vuông ABCD cạnh a. Lấy M thuộc AB, N thuộc AD sao cho AM + AN + MN = 2a. Chứng minh \(\widehat {MCN} = 45^\circ \).
Quảng cáo
Trả lời:
Giải bởi Vietjack
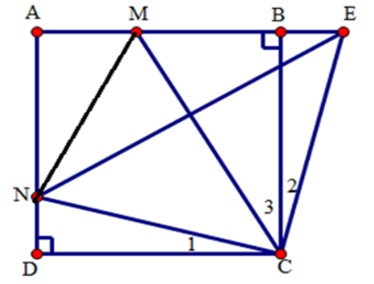
Vẽ tia Cx vuông góc với CN tại C, cắt AB tại E.
\(\widehat {{C_1}} + \widehat {MCN} + \widehat {{C_3}} = 90^\circ \)
\(\widehat {{C_2}} + \widehat {MCN} + \widehat {{C_3}} = 90^\circ \)
Suy ra: \(\widehat {{C_1}} = \widehat {{C_2}}\)
Xét tam giác CDN và tam giác CBE có:
\(\widehat {{C_1}} = \widehat {{C_2}}\)
CD = CB
\[\widehat {CDN} = \widehat {CBE} = 90^\circ \]
⇒ ∆CDN = ∆CBE (c.g.c)
⇒ CN = CE; DN = BE
Xét: AM + AN + ME
= AM + AN + MB + BE
= AM + AN + MB + ND (vì BE = ND, chứng minh trên)
= AM + MB + AN + ND
= AB + AD = 2a
Suy ra: AM + AN + ME = AM + AN + MN = 2a
Vậy MN = ME
Xét tam giác CMN và tam giác CME có:
CN = CE
Chung CM
MN = ME
⇒ ∆CMN = ∆CME (c.c.c)
⇒ \(\widehat {MCN} = \widehat {ECM}\)
Mà \(\widehat {MCN} + \widehat {ECM} = 90^\circ \)(do CE vuông góc CN)
Vậy \(\widehat {MCN} = 45^\circ \).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(\tan \left( {\alpha - \frac{\pi }{4}} \right) = \frac{{\tan \alpha - \tan \frac{\pi }{4}}}{{1 + \tan \alpha .\tan \frac{\pi }{4}}} = \frac{{2 - 1}}{{2 + 1}} = \frac{1}{3}\).
Lời giải
Tính được: 270° = \(\frac{{270}}{{180}}\pi = \frac{3}{2}\pi = \frac{3}{4}.2\pi \)
Vậy đu quay được góc 270° khi nó quay được \(\frac{3}{4}\) vòng
Ta có: đu quay quay được 1 vòng trong \(\frac{1}{3}\) phút
Vậy đu quay đu được \(\frac{3}{4}\) vòng trong: \(\frac{3}{4}.\frac{1}{3} = \frac{1}{4}\) phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo