Câu hỏi:
29/01/2024 607
Cho hình vuông ABCD tâm O, trên đoạn BC lấy điểm E bất kì, trên tia đối của tia CD lấy điểm F sao cho CE = CF.
a) Chứng minh DE = BF.
b) Tia DE cắt BF tại H. Chứng minh \(\widehat {DHF} = 90^\circ \).
c) Gọi I là trung điểm của EF, K là giao điểm của FE và BD. Chứng minh tứ giác AOIK là hình bình hành.
d) Chứng minh A, H, K thẳng hàng.
Cho hình vuông ABCD tâm O, trên đoạn BC lấy điểm E bất kì, trên tia đối của tia CD lấy điểm F sao cho CE = CF.
a) Chứng minh DE = BF.
b) Tia DE cắt BF tại H. Chứng minh \(\widehat {DHF} = 90^\circ \).
c) Gọi I là trung điểm của EF, K là giao điểm của FE và BD. Chứng minh tứ giác AOIK là hình bình hành.
d) Chứng minh A, H, K thẳng hàng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
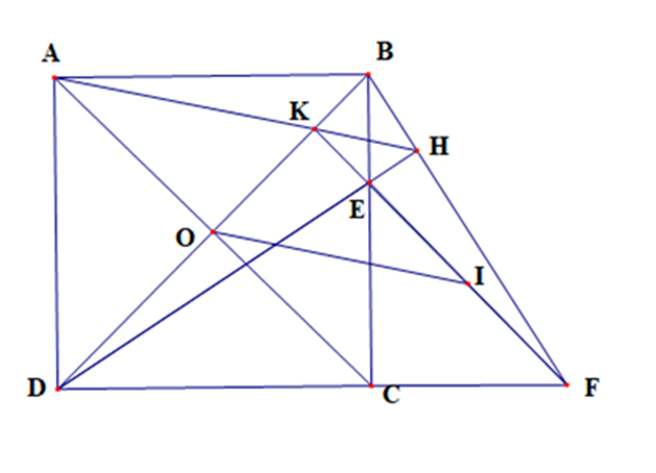
a) Vì ABCD là hình vuông nên AB = BC = CD = DA và
\[\widehat {ABC} = \widehat {BCD} = \widehat {CDA} = \widehat {DAB} = 90^\circ \]
Xét △DEC và △BFC có
EC = FC (giả thiết)
\[\widehat {DCE} = \widehat {BCF} = 90^\circ \]
DC = BC (chứng minh trên)
Do đó △DEC = △BFC (c.g.c)
Suy ra DE = BF (2 cạnh tương ứng), \[\widehat {EDC} = \widehat {FBC}\]
b) Xét △BEH và △DEC có
\[\widehat {BEH} = \widehat {DEC}\] (hai góc đối đỉnh)
\[\widehat {EDC} = \widehat {FBC}\] (chứng minh câu a)
Suy ra △BEH ∽ △DEC (g.g)
Do đó \[\widehat {BHE} = \widehat {DCE}\]
Mà \[\widehat {DCE} = 90^\circ \]nên \[\widehat {BHE} = 90^\circ \]
Hay DE ⊥ BF
Suy ra \[\widehat {DHF} = 90^\circ \]
c) Xét tam giác BDF có
DE ⊥ BF
BC ⊥ DF
DE cắt BC tại E
Suy ra E là trực tâm tam giác BDF
Do đó FK ⊥ BD
Mà AO ⊥ BD
Suy ra AO // IK
Vì CE = CF nên tam giác CEF cân tại C
Mà CI là trung tuyến
Suy ra CI là đường cao
Hay CI ⊥ EF
Xét tứ giác OKIC có \[\widehat {OKI} = \widehat {KOC} = \widehat {CIK} = 90^\circ \]
Suy ra OKIC là hình chữ nhật
Do đó OC = KI
Mà OC = AO
Suy ra AO = KI
Xét tứ giác AOIK có AO // KI, AO = KI (chứng minh trên)
Suy ra AOIK là hình bình hành
d) Xét tứ giác ABHD có \[\widehat {BAD} + \widehat {BHD} = 90^\circ + 90^\circ = 180^\circ \]
Suy ra tứ giác ABHD nội tiếp
Do đó \[\widehat {AHB} = \widehat {ADB} = 45^\circ \]
Xét tứ giác DKHF có \[\widehat {DKF} = \widehat {DHF} = 90^\circ \]
Suy ra tứ giác DKHF nội tiếp
Do đó \[\widehat {KHB} = \widehat {FDB} = 45^\circ \]
Suy ra \[\widehat {AHB} = \widehat {KHB}\]
Suy ra AH ≡ KH
Do đó A, H, K thẳng hàng.
Vậy A, H, K thẳng hàng.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025)
Đã bán 1,1k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tanα = 2. Tính \(\tan \left( {\alpha - \frac{\pi }{4}} \right)\).
Cho tanα = 2. Tính \(\tan \left( {\alpha - \frac{\pi }{4}} \right)\).
Xem đáp án »
13/07/2024
32,202
Câu 2:
Cho tam giác ABC nhọn nội tiếp (O). Kẻ đường cao AD của tam giác ABC, đường kính AK của đường tròn (O). Gọi E và F lần lượt là hình chiếu của B và C trên AK. Gọi M và N lần lượt là trung điểm của BC và AC. Chứng minh: MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF.
Cho tam giác ABC nhọn nội tiếp (O). Kẻ đường cao AD của tam giác ABC, đường kính AK của đường tròn (O). Gọi E và F lần lượt là hình chiếu của B và C trên AK. Gọi M và N lần lượt là trung điểm của BC và AC. Chứng minh: MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF.
Xem đáp án »
13/07/2024
28,773
Câu 3:
Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay quay được góc 270°?
Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay quay được góc 270°?
Xem đáp án »
13/07/2024
27,807
Câu 4:
1 thùng rỗng nặng 1 yến. Khi đổ đầy nước thì thùng nước đó nặng 120kg. Hỏi một nửa thùng đó nặng bao nhiêu?
1 thùng rỗng nặng 1 yến. Khi đổ đầy nước thì thùng nước đó nặng 120kg. Hỏi một nửa thùng đó nặng bao nhiêu?
Xem đáp án »
13/07/2024
13,225
Câu 6:
Cho một cấp số nhân có công bội bằng 3 và số hạng đầu bằng 5. Biết số hạng chính giữa là 32805. Hỏi cấp số nhân đã cho có bao nhiêu số hạng?
Cho một cấp số nhân có công bội bằng 3 và số hạng đầu bằng 5. Biết số hạng chính giữa là 32805. Hỏi cấp số nhân đã cho có bao nhiêu số hạng?
Xem đáp án »
13/07/2024
8,868
Câu 7:
Cho hình trên biết AB // CD, CD // EF. Tính \(\widehat {ACD}\) và \(\widehat {ACE}\).
Cho hình trên biết AB // CD, CD // EF. Tính \(\widehat {ACD}\) và \(\widehat {ACE}\).
Xem đáp án »
13/07/2024
5,790
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận