Câu hỏi:
13/07/2024 604
Tam giác ABC nội tiếp (O), AD là đường kính của (O). M là trung điểm của của BC, H là trực tâm của tam giác ABC. Gọi X, Y, Z lần lượt là hình chiếu vuông góc của D lên HB, HC, BC. Chứng minh rằng 4 điểm X, Y, Z, M cùng thuộc 1 đường tròn.
Tam giác ABC nội tiếp (O), AD là đường kính của (O). M là trung điểm của của BC, H là trực tâm của tam giác ABC. Gọi X, Y, Z lần lượt là hình chiếu vuông góc của D lên HB, HC, BC. Chứng minh rằng 4 điểm X, Y, Z, M cùng thuộc 1 đường tròn.
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
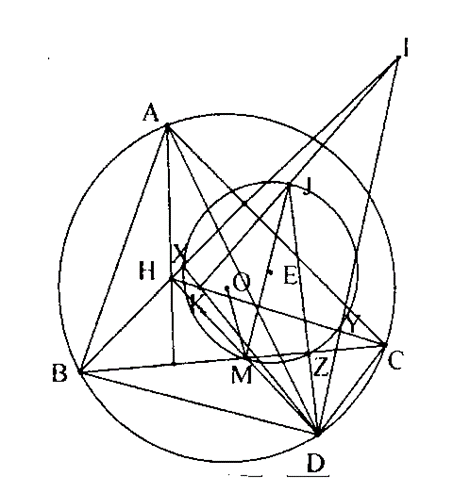
Giả sử HB cắt DY tại I, HC cắt DX tại K, J là trung điểm IK
Xét tam giác ADC có \(\widehat {ACD} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Nên AC ⊥ CD
Mà BH ⊥ AC. Nên BH // CD
Tương tự: \(\widehat {ABD} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Nên AB ⊥ BD
Mà CH ⊥ AB nên CH // BD
Xét tứ giác BHCD có: BH // CD và CH // BD nên BHCD là hình bình hành.
⇒ HD, BC cắt nhau tại trung điểm M của mỗi đường
Vì DX ⊥ HI, DI ⊥ HC suy ra K là trực tâm của tam giác IHD
Nên: \[\widehat {KDI} = \widehat {KHI} = \widehat {HCD}\](HI //CD)
\(\widehat {CHD} = \widehat {KID}\)(cùng phụ với \(\widehat {HDI}\))
Xét tam giác KID và tam giác CHD có:
\(\widehat {KID} = \widehat {CHD}\)
\[\widehat {KDI} = \widehat {HCD}\]
⇒ ∆KID ∽ ∆CHD (g.g)
Mặt khác CM, DJ là hai trung tuyến tương ứng của tam giác CHD và KID
Như vậy ta có: ∆DIJ ∽ ∆CHM
⇒ \[\widehat {JDI} = \widehat {HCM}\]
Từ đó suy ra: DJ vuông góc với BC tại Z hay Z thuộc đường tròn đường kính MJ.
Lại có: M là trung điểm HD (chứng minh trên)
X, Y, Z lần lượt là hình chiếu vuông góc của D lên HB, HC, BC
Kết hợp tính chất điểm M thì đường tròn đường kính MJ là đường trò Ơ–le của tam giác HID.
Suy ra: X, Y, Z, M cùng thuộc 1 đường tròn.
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tanα = 2. Tính \(\tan \left( {\alpha - \frac{\pi }{4}} \right)\).
Cho tanα = 2. Tính \(\tan \left( {\alpha - \frac{\pi }{4}} \right)\).
Xem đáp án »
13/07/2024
31,819
Câu 2:
Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay quay được góc 270°?
Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay quay được góc 270°?
Xem đáp án »
13/07/2024
26,149
Câu 3:
Cho tam giác ABC nhọn nội tiếp (O). Kẻ đường cao AD của tam giác ABC, đường kính AK của đường tròn (O). Gọi E và F lần lượt là hình chiếu của B và C trên AK. Gọi M và N lần lượt là trung điểm của BC và AC. Chứng minh: MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF.
Cho tam giác ABC nhọn nội tiếp (O). Kẻ đường cao AD của tam giác ABC, đường kính AK của đường tròn (O). Gọi E và F lần lượt là hình chiếu của B và C trên AK. Gọi M và N lần lượt là trung điểm của BC và AC. Chứng minh: MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF.
Xem đáp án »
13/07/2024
18,119
Câu 4:
1 thùng rỗng nặng 1 yến. Khi đổ đầy nước thì thùng nước đó nặng 120kg. Hỏi một nửa thùng đó nặng bao nhiêu?
1 thùng rỗng nặng 1 yến. Khi đổ đầy nước thì thùng nước đó nặng 120kg. Hỏi một nửa thùng đó nặng bao nhiêu?
Xem đáp án »
13/07/2024
13,054
Câu 5:
Cho một cấp số nhân có công bội bằng 3 và số hạng đầu bằng 5. Biết số hạng chính giữa là 32805. Hỏi cấp số nhân đã cho có bao nhiêu số hạng?
Cho một cấp số nhân có công bội bằng 3 và số hạng đầu bằng 5. Biết số hạng chính giữa là 32805. Hỏi cấp số nhân đã cho có bao nhiêu số hạng?
Xem đáp án »
13/07/2024
8,720
Câu 7:
Cho hình trên biết AB // CD, CD // EF. Tính \(\widehat {ACD}\) và \(\widehat {ACE}\).
Cho hình trên biết AB // CD, CD // EF. Tính \(\widehat {ACD}\) và \(\widehat {ACE}\).
Xem đáp án »
13/07/2024
5,719
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận