Câu hỏi:

19/08/2025 2,741

Cho tam giác ABD có AB = 15cm, AD = 20cm, BD = 25cm. Vẽ AM vuông góc BD.

a) Chứng minh: tam giác ABD vuông. Tính AM, BM, MD.
b) Kẻ tia Bx // AD, vẽ AM vuông góc BD cắt Bx tại C. Chứng minh: AB² = AD.BC.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

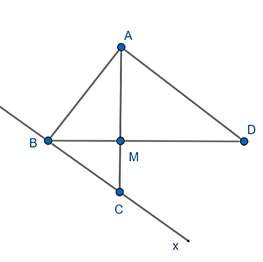
Cho tam giác ABD có AB = 15cm, AD = 20cm, BD = 25cm (ảnh 1)

a) Ta thấy: 25² = 20² + 15² hay AB² + AD² = BD²

Theo định lí Pytago đảo, suy ra tam giác ABD vuông tại A

Áp dụng hệ thức lượng trong tam giác ABD vuông ta có:

AB.AD = AM.BD ⇒ AM = \(\frac{{AB.AD}}{{BD}} = \frac{{15.20}}{{25}} = 12cm\)

AD² = MD.BD ⇒ DM = \(\frac{{A{D^2}}}{{BD}} = \frac{{{{20}^2}}}{{25}} = 16cm\)

BM = BD – DM = 25 – 16 = 9(cm)

b) Vì AB ⊥ AD do ABD vuông tại A

Và Bx // AD

Nên Bx ⊥ AB tại B. Suy ra: \(\widehat {ABC} = 90^\circ \)

Xét tam giác BAM và tam giác BDA có:

Chung \(\widehat B\)

\(\widehat {BMA} = \widehat {BAD} = 90^\circ \)

⇒ ∆BMA ∽ ∆BAD (g.g)

Suy ra: \(\widehat {BAM} = \widehat {BDA}\) hay \(\widehat {BAC} = \widehat {BDA}\)

Xét tam giác BAC và tam giác BAD có:

\(\widehat {BAC} = \widehat {BDA}\)(chứng minh trên)

\(\widehat {ABC} = \widehat {BAD} = 90^\circ \)

⇒ ∆BAC ∽ ∆ADB (g.g)

⇒ \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\) ⇒ AB² = AD.AC.

Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay quay được góc 270°?

Lời giải

Tính được: 270° = \(\frac{{270}}{{180}}\pi = \frac{3}{2}\pi = \frac{3}{4}.2\pi \)

Vậy đu quay được góc 270° khi nó quay được \(\frac{3}{4}\) vòng

Ta có: đu quay quay được 1 vòng trong \(\frac{1}{3}\) phút

Vậy đu quay đu được \(\frac{3}{4}\) vòng trong: \(\frac{3}{4}.\frac{1}{3} = \frac{1}{4}\) phút.

Câu 2

Cho tam giác ABC nhọn nội tiếp (O). Kẻ đường cao AD của tam giác ABC, đường kính AK của đường tròn (O). Gọi E và F lần lượt là hình chiếu của B và C trên AK. Gọi M và N lần lượt là trung điểm của BC và AC. Chứng minh: MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF.

Lời giải

Cho tam giác ABC nhọn nội tiếp (O). Kẻ đường cao AD của tam giác (ảnh 1)

Xét ADFC có: \(\widehat {ADC} = \widehat {AFC} = 90^\circ \)(Vì AD ⊥ BC và CF ⊥ AK)

Suy ra: ADFC nội tiếp vì 2 góc cùng nhìn AC dưới 1 góc 90° không đổi.

⇒ \(\widehat {DFA} = \widehat {DCA}\)(cùng chắn cung AD) hay \(\widehat {DFA} = \widehat {BCA}\)

Mà \(\widehat {BKA} = \widehat {BCA}\)(góc nội tiếp)

Suy ra: \(\widehat {DFA} = \widehat {BKA}\)

Mà 2 góc \(\widehat {DFA};\widehat {BKA}\)ở vị trí đồng bị nên DF // BK

Mà BK ⊥ AB nên DF ⊥ AB

Mặt khác MN // AB (MN là đường trung bình của tam giác ABC)

Suy ra: MN ⊥ DF (đpcm).

Lại có: MN ⊥ DF

⇒ EM ⊥ DF

AK là đường kính, BC là đây cung (1)

⇒ AK ⊥ BC hay DM ⊥ DF (2)

Từ (1) và (2) suy ra: M là tâm đường tròn ngoại tiếp tam giác DEF.

Câu 3